1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

解析 I 定積分

これまで求めてきた導関数; $\begin{align}f'(x) = \lim_{\Delta x\rightarrow 0} \frac{f( x+{\Delta x} ) - f(x)}{\Delta x} \end{align}$ は、「 $x$ から $x+{\Delta x}$ にかけての増加率 $\displaystyle {\Delta y \over \Delta x}$ を詳しくしたもの」でした。 $\begin{align}f'(x) = \lim_{\Delta x\rightarrow 0} \frac{ \Delta y }{\Delta x} \end{align}$ ${\Delta x}$ は $x$ の増えた分（増分）、 ${\Delta y}$ は $y$ の増えた分です。

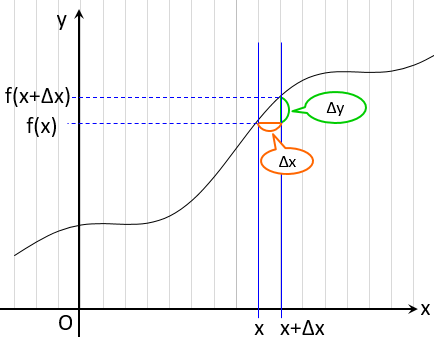
この式は、 $\displaystyle \lim_{\Delta x\rightarrow 0}$ を使わないで書くと、このようにも書けます。
$\begin{align} \frac{\Delta y}{\Delta x} \rightarrow f'(x) \qquad（{\Delta x \rightarrow 0} のとき） \end{align}$ この式の両辺に $\Delta x$ をかけるとこうなります。
$\begin{align} \Delta y \rightarrow f'(x) {\Delta x} \qquad（{\Delta x \rightarrow 0} のとき） \end{align}$ つまり、上の図の $\Delta y$ は、 $f'(x)$ と $\Delta x$ でわかるということですね。

さて、この $\Delta y$ は、 $x$ から $x+{\Delta x}$ までの区間の $y$ の増分でしたが、
この前の区間とか、これの次の区間とかについても、
同じように $y$ の増分 $\Delta y$ を求めることができます。

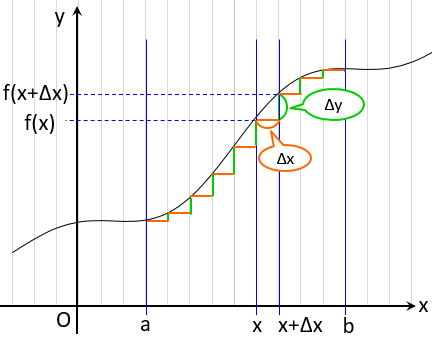
これを、 $x=a$ から $x=b$ までのたくさんの区間について
全部足し算したらどうでしょう？すこしづつ増えた $\Delta y$ を
全部積み重ねていくことになります。

ちなみに「 $x=a$ から $x=b$ までについて全部足す」
を表す記号が $\displaystyle \sum_{x=aから}^{x=bまで}$ です。「総和」ともいいます。
英語で言うとsum（合計）です。頭文字 S です。
英文字の Sに対応するギリシア文字が $\Sigma$ です。シグマと呼んでます。
$\begin{align} \sum_{x=aから}^{x=bまで} \Delta y \rightarrow \sum_{x=aから}^{x=bまで} 　f'(x) {\Delta x}　\quad \qquad（{\Delta x \rightarrow 0} のとき） \end{align}$ $\Delta y$ の総和は、 $f'(x) {\Delta x}$ の総和に近づくってこどです。

次の図を見て分かる通り、 $\Delta y$ の総和は、 $f(b)-f(a)$ になりますね。

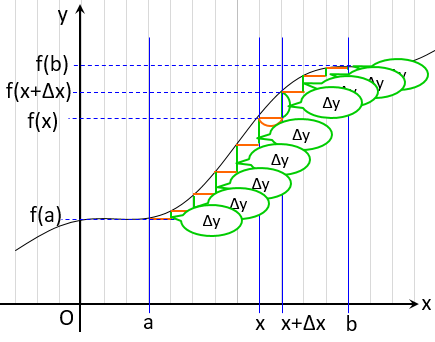
よって
$\begin{align} \sum_{x=aから}^{x=bまで} 　f'(x) {\Delta x}　\quad \rightarrow f(b) - f(a) \qquad（{\Delta x \rightarrow 0} のとき） \end{align}$ ここで注目は ${\Delta x \rightarrow 0}$ です。 $\Delta x$ を無限に細かくしています。

ただ足すだけでなく、 $\Delta x$ を無限に細かく分けて足すとき、
ギリシア文字 $\Delta$ を英語の d に替えて $\Delta x$ を $dx$ と書き、
ギリシア文字 $\Sigma$ を英語の S を縦に引っ張った形に替えて
$\displaystyle \sum_{x=aから}^{x=bまで}$ を $\displaystyle \int_{x=aから}^{x=bまで}$ と書きます。これを使ったらもう
${\Delta x \rightarrow 0}$ は書かなくていいです。よって
$\begin{align} \int_{x=aから}^{x=bまで} 　f'(x) \ dx \quad = f(b) - f(a) \end{align}$ これを $f'(x)$ の定積分と言います。
$f'(x)dx$ をちょっとずつ足していくと $f(a)$ から $f(b)$ まで増える
ということを表しています。

左辺の中身 $f'(x)$ は導関数ですね。微分してあります。
一方、右辺は $'$ がついておらず、微分前の元の関数 $f(x)$ です。
しかも最初の $x=a$ における値と最後の $x=b$ における値の差です。

右辺は、 $f(b) - f(a)$ と同じ式 $f$ を2回書くのは面倒なのでこれを
$\Bigl[ \ f(x) \ \Bigr] _{x=aから}^{x=bまで}$ と書いてもいいことになっています。
$\Bigl[ \ f(x) \ \Bigr] _{x=aから}^{x=bまで} = f(b)- f(a)$ です。終着点 $x=b$ の値を代入した式から、
出発点 $x=a$ を代入した式の引き算を表します。

これを使うと $\begin{align} \int_{x=aから}^{x=bまで} 　f'(x) \ dx \quad = \quad \Bigl[ \ f(x) \ \Bigr] _{x=aから}^{x=bまで} \end{align}$ と書くことができます。

以上まとめると

$\begin{align} \int_{x=aから}^{x=bまで} 　(微分後) \ dx \quad = \quad \Bigl[ 微分前 \Bigr]_{x=aから}^{x=bまで} \end{align}$
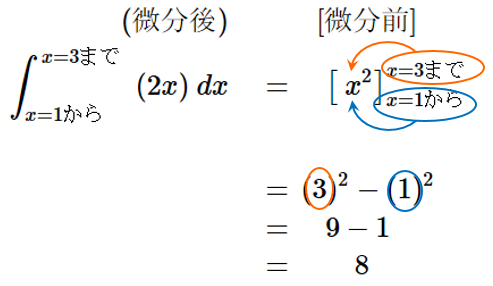
使用例: 答えが数字になりましたね。このように、 $x=$ 出発点と $x=$ 終着点が
指定されている定積分の答えは、式ではなく数字になります。
積分記号をノートに書くときは: 積分記号や、代入のための\Bigl[ \Bigr] は「大型記号」といい、必ず２行使って書くのが決まりです。
２行使って書いたら、間を１行あけて、次にまた２行使って書いていきます。
高校では $x=$ と書かなかった: 高校で積分をやった方は、 $\begin{align} \int_{x=1から}^{x=3まで}(2x) \ dx \, &= \, \Bigl[ \ x^2 \Bigr] _{x=1から}^{x=3まで} \end{align}$ とは書かずに、 $x=$ など付けないで $\begin{align} \int_{1}^{3}(2x) \ dx \, &= \, \Bigl[ \ x^2 \Bigr] _{1}^{3} \end{align}$ と書いていたと思います。高校の時は、1変数関数しか扱わないので、 $x$ だけとか $t$ だけしか出てこないから困らなかったのですが、大学では $\begin{align} \int_{z=-d}^{z=d} \, \int_{y=0}^{y=1} \, \int_{x=-1}^{x=1} \, f(x,y,z) \ dx \ dy \ dz \end{align}$ とか $\begin{align} \int_{r=0}^{\infty} \, \int_{\theta = -{\pi \over 2}}^{\theta = -{\pi \over 2}} \, \int_{\phi=0}^{\phi = 2\pi} \, f( r, \phi, \theta) \ dr , d\phi, d\theta \end{align}$ のように、多変数の積分を行うようになりますので、
どれにどれを代入するのか混乱しがちです。

1年前期では困らないのですが、今後の勉強での混乱を避けるために、
$x=$ を書いておくことをお勧めします。
（ただし $\infty$ の時はイコールを書かないこと）

早速使ってみよう