情報通信工学科１年　解析（中川） 宿題9（増減表とグラフ）

増減表を書いてグラフを描きなさい。

(12) y = e^-ax sin( x ) ただし a = 1/√3, 範囲は 0< x< 2π

y ' = ( e^-ax)' sin( x ) + e^-ax { sin( x ) }'
　　 = -ae^-ax sin( x ) + e^-ax cos( x )
　　 = e^-ax { -a sin( x ) + cos( x ) }

e^-ax は常にプラスなので、
傾き y ' が＋になるのは { -a sin( x ) + cos( x ) } が＋の時

-a sin( x ) + cos( x ) = A sin( x + φ) とおくと
-a sin( x ) + cos( x ) = A sin x cosφ+ A cos x sinφ だから
A cosφ = -a = - 1/√3
A sinφ = 1
それぞれ２乗して足すと
（左辺）=( A cosφ )² + ( A sinφ )²= A²
(右辺)= a² + 1 = 4/3
よって
A=2/√3 (Aにはプラスを選ぶ）
よって
cosφ = -a /A = -1 /2
sinφ = 1 / A = √3 /2
両方を満たすφは120度すなわち 2π/3
よって-a sin( x ) + cos( x ) = 2/√3{ sin( x + 2π/3 ) }
よって y ' = 2/√3 e^-ax { sin( x + 2π/3 ) }

傾き y ' が＋になるのは sin( x + 2π/3 ) が + の時

つまり
0< x + 2π/3 <π ,
2π< x + 2π/3 <3π ,
:
のとき、すなわち
- 2π/3< x <π/3 ,
4π/3< x <7π/3 ,
:
だが、問題の範囲が 0< x< 2πだから
0 < x <π/3 と 4π/3< x <2π でy’がプラス
傾き y ' が0になるのは x = π/3 と x = 4π/3

x = π/3のときy= e^-π/3√3sin(π/3) = (√3/2) e^-π/3√3

x = 4π/3のときy= e^-4π/3√3sin(4π/3) = (-√3/2) e^-4π/3√3

これらを増減表にかくと

x	0		π/3		4π/3		2π
傾き y'	+	+	0	-	0	+	+
グラフ y	0	／ 増加	極大値	＼ 減少	極小値	／ 増加	0

極大値 (√3/2) e^-π/3√3
極小値 (-√3/2) e^-4π/3√3
x=π のとき y=0 などの点も参考にグラフを描く

y '' = 4/3 e^-ax { sin( x + 4π/3 ) }
x = 2π/3, 5π/3 で y''=0

x	0		π/3		2π/3		4π/3		5π/3		2π
傾き y'	+	+	0	-	-	-	0	+	+	+	+
y ''	-	-	-	-	0	+	+	+	0	-	-
グラフ y	0	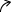増加	極大値	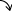減少	変曲点	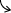減少	極小値	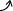増加	変曲点	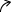増加	0

　　　　　　　　x=2πのとき、y=0でも傾きは０でないことに注意