情報通信工学科１年　解析（中川） 宿題9（増減表とグラフ）

増減表を書いてグラフを描きなさい。

(3) y = -2 x³ + 6 x² - 1 　　（少し慣れた初心者向き）

y ' = -6x² +12 x
　　 = -6 ( x² -2 x )
　　 = -6x（x - 2）

傾き y ' が＋になるのは -6x（x - 2） が＋の時　つまり x（x - 2）が - になるとき。

(i) x >0　かつ　x - 2 < 0 のとき
　つまり x > 0　かつ　 x < 2のとき
　つまり 　0 < x < 2のとき

(ii) x <0　かつ　x - 2 >0 のとき
　つまり x < 0　かつ　 x > 2のとき
　これは　ありえない

傾き y ' が - になるのは -6x（x - 2） が - の時 つまり x（x - 2）が + になるとき。

(iii) x >0　かつ　x - 2 >0 のとき
　つまり x>0　かつ　 x>2のとき
　つまり 　x > 2のとき

(iv) x <0　かつ　x - 2 < 0 のとき
　つまり x<0　かつ　 x<2のとき
　つまり 　x < 0 のとき

傾き y ' が ０ になるのは

　x =0　または　x =2 のとき

これらを増減表に書くと

x		0		2
傾きy'	-	0	+	0	-
グラフy	＼ 減少	極小 -1	／ 増加	極大 7	＼ 減少

極大値を求めると
x=0 のとき y = -2 ・0³ + 6・0² - 1 = -1

極小値を求めると
x=2 のとき y = -2 ・2³ + 6・2² - 1 = 7

これらを増減表に記入　　　　..........................

曲率も求めるなら

y ' ' = ( -6x² +12 x ) '
　　 = - 12x+12
　　 = -12 (x－1)

y ' ' が＋になるのは
-12 (x－1)>0 のとき、つまり　
　- (x－1)>0 のとき、つまり　
1> x のとき（下に凸）。

y ' ' が - になるのは
x-1<0 のとき、つまり　x < 1 のとき（上に凸）。

y ' ' が 0 になるのは
x-1=0 のとき、つまり　x =　1 のとき（変曲点）。
変曲点を求めると
x=1のとき y = -2 ・1³ + 6・1² - 1 =

これらを増減表に加えると

x		0		1		2
傾き y'	-	0	+	+	+	0	-
曲率 y' '	+	+	+	0	-	-	-
グラフ y	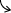減少	極小 -1	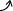増加	変曲点	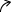増加	極大 7	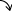減少