(1) f(x) = x e^-ax とおくと

f(x) ' = (x)' e^-ax + x ( e^-ax )'
　　 = 　　 e^-ax + x ( -ae^-ax )　　ここ（　）ないと不可
　　 = 　　 e^-ax(1-ax)

e^-ax は常に正(+)なので、(1-ax) > 0 のとき f(x) ' が＋
　両辺にaxを足して 1-ax + ax > 0+ax つまり
　　　　　　　　　 1 　　> ax 　ここでaは正(+)なので両辺をaで割って
　　　　　　　　　　(1/a)　> x のとき f(x) ' が＋

e^-ax は常にプラスなので、(1-ax) < 0 のとき f(x) ' が負(-)
　　　　　　　　　　つまり (1/a) < x のとき f(x) ' が負(-)

これらを増減表にかくと

x	(1/a)より小	1/a	(1/a)より大
傾きf(x)'	+	0	-
グラフ y	／ 増加	極大値 1/(ae)	＼ 減少

極大値はf(x)にx=1/a を代入して f(1/a) = (1/a)e^-1=1/(ae)

グラフの右半分ではｘは＋, 指数関数は常に＋　なので マイナスになりません

傾きの増加率も求める

f(x) ' ' = { e^-ax (1-ax) } '
　　　 = ( e^-ax )' (1-ax) + e^-ax (1-ax)'
　　　 = -ae^-ax (1-ax) + e^-ax (-a)
　　　 = e^-ax (-a+a²x) + e^-ax (-a)
　　　 = e^-ax (a²x-2a)
　　　 = a² e^-ax (x-2/a)
a² e^-ax は常にプラスなので、
f(x) ' ' が＋になるのは x-2/a > 0 のとき。
　　　　　　　つまり x > 2/a のとき（下に凸）。
f(x) ' ' が - になるのは x-2/a < 0 のとき。
　　　　　　　つまり x < 2/a のとき（上に凸）。
f(x) ' ' が 0 になるのは x-2/a =　0 のとき（変曲点）。
　　　つまり x = 2/a のとき。
これらを増減表に加えると 　

x		1/a		2/a
傾きf(x) '	+	0	-	-	-
曲率f(x) ' '	-	-	-	0	+
グラフ y	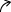増加	極大値 1/(ae)	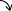減少	変曲点 2/(ae2)	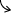減少

　　　　　　　　　　　　　　　変曲点のyの値は
　　　f(x) のxに 2/a を代入して f(2/a) = (2/a) e^-2