| 離散フーリエ変換(DFT) |
| 前のページから |
am = (2/N) Σk=0N-1{ fk cos(2mpk/N) } でamを求められるのは、 fk に含まれているcos(2mpk/N)波成分と、 後ろからかけた cos(2mpk/N)波成分が反応して cos2(2mpk/N) になり、 これを1周期積分するとN/2 になるからなのでした。 ここで、m=N/2 のとき[一番細かい波:データ2個で1つの波を表す)は注意が必要です。 例えば、N=4で a2 を求めたいとき。 fk に含まれている 2個1周期(2山)のcos(2・2pk/4)波成分(黒い線)と、 後ろからかけた 2個1周期(2山)のcos(2・2pk/4)波成分(黒い線)の掛け算は、 波形を描いてみると、 お互いマイナス同士のところがプラスになるので、 2山でなく4山になっています(ピンクのところ)。 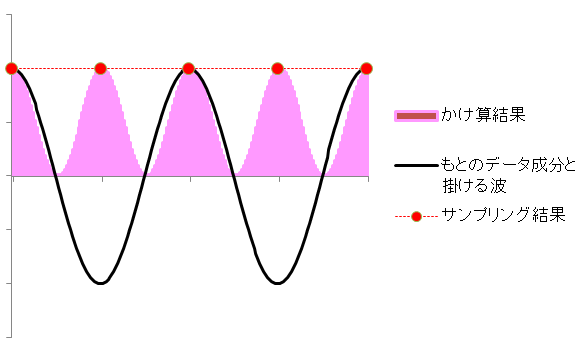 本当の積分だったら、その山の形の沿って(ピンクで塗ったとこ)面積を出せるのですが、 長方形で近似した面積(点線)だと、 山の頂上の間隔がデータの間隔(サンプリング間隔)と同じになってしまったため(赤丸つけたとこ)、 凹んでる部分を飛ばしてしまって、面積が2倍になってしまうのです。 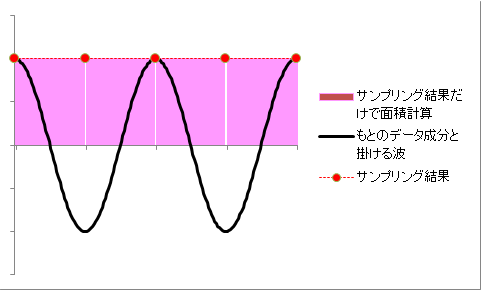 N=128で a64 を求めたいとき、 N=1024で a512 を求めたいとき、...も同じことが起こります。 凹みを表すための点がないので、 この式をそのまま使っていると、m=N/2 のときだけ値が2倍になってしまいます。 そのため、 m=0 の時だけでなく、 m= N/2 の時も、 最初の(2/N)のとこを(1/N)にしないといけなかったのです。 よって am = (2/N) Σk=0N-1{ fk cos(2mpk/N) } ただしm=0, または m=N/2 のときは am = (1/N) Σk=0N-1{ fk cos(2mpk/N) } N=4個の実例へ戻る |