| コンピュータ数値解析 台形公式 |
|
f(x) = exp( -x2) を x = 0 から x = 100とか x = 260とかまで積分したとき、
台形公式なのに、誤差や「前の計算値との差」が、
刻み幅hの2乗で減らない(刻み幅hを半分にしたのに差が1/4にならない)ことがありますね。 | ||||
|
減り方が遅い (1/4倍でなく 1/2倍で減る) |
次の例では、刻み幅hを半分にしていったとき、
「前の計算値との差」が、1/4にならないで半分になってますよね。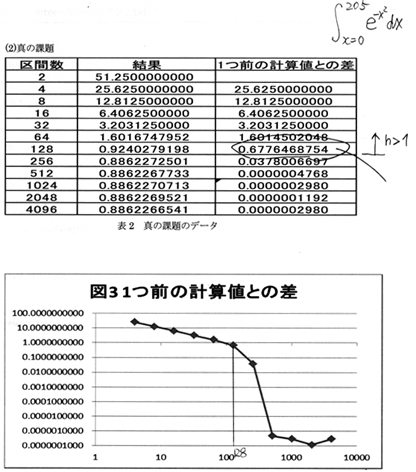 この理由は、刻み幅 h が粗すぎる(1より大きい)ためです。 上の例は x = 0 から x = 205までの積分なので、 刻み幅 h = ( 区間幅 205 ) / ( 区関数 n ) ですから、 nが205より小さいと、h は1より大きいです。 | |||
|
誤差がh2に 比例するのは |
台形公式とは、台形1本分の幅のグラフ f(x)の
テイラー展開の式を
( x-xk ) の1次の式までで打ち切って f(x) 〜 c0 + c1( x-xk ) 」 + c2( x-xk )2 + c3( x-xk )3 + c4( x-xk )4 + ... (ここで打ち切り) x = xk から x = xk+h まで積分したものなので、 打ち切られたあとの部分が誤差になり、 台形1本につき ∫xkxk+h { c2( x-xk )2 + c3( x-xk )3 + c4( x-xk )4 + ... } dx の誤差が出ます。 実際に積分すると、台形1本あたりの誤差は = [ c2( x-xk )3/3 + c3( x-xk )4/4 + c4( x-xk )5/5 + ... ]xkxk+h = { c2 h3/3 + c3 h4/4 + c4 h5/5 } + ... となります。 |
c2 = f''(xk)/2! c3 = f'''(xk)/3! テイラー展開 | ||
|
h < 1 なら |
ここで、h が1より小さければ、
何度もかけるとすごく小さくなるため、 かけた回数の少ない、最初のh3が最も大きい誤差となります。 それがn本分あるため、全体でおよそ n h3の誤差となります。 n h3 = nh h2 ここで、h=(b-a)/n を思い出すと、nh=(b-a) は定数、よって 台形公式の誤差は、だいたい h2に比例することがわかります。 | |||
|
h > 1 だと |
しかし、もし、刻みが荒すぎて、h が1より大きいと、
1番めよりもむしろ後ろのほうの項が大きくなってしまうため、
「台形公式らしい」動きをしなくなってしまうのです。
| |||
|
誤差(差)が 急に 減るのは |
上の例をみると、n=256を超えると、急に差が減り、 h2よりずっと激しく減っています。
これはなぜでしょう。 さっきの台形1本当たりの誤差に、テイラー展開の係数 c2、 c3、... を代入して 台形n本分合計すると、 Σk=0n-1 { (f''(xk)/2!) h3/3 + (f'''(xk)/3!) h4/4 + f''''(xk)/4!) h5/5 + ... } =Σk=0n-1 f''(xk) h3/3! +Σk=0n-1 f'''(xk) h4/4! +Σk=0n-1 f''''(xk) h5/5!+ ... ここで最初の Σk=0n-1 f''(xk) h3/3! を Σk=0n-1 f''(xk) h と h2/3! に分けてみてください。 Σk=0n-1 f''(xk) h は、 f''(xk)に幅h をかけてn本足してるので、 f''(x)の定積分です。 f''(x)を 積分したらf'(x)です。 積分区間aからbまでなら、定積分の結果は [f'(x)]x=ax=b= f'(b)-f'(a)です。 てことは、台形公式の誤差は { f'(b)-f'(a) } h2/3! に比例する感じになるわけです。
f'(b) = f'(a) |
だと
ここでもしf'(b) = f'(a) だと、この項自体が消えてしまい、
誤差がh2ではなく、 |
もっと後ろの項h4に比例するようになります。 f(x) = exp( -x2) の場合、 f'(0) = 0 ですし、また、 xが(100とか200とか)大きくなるとやっぱり f'(x)→ 0 に近づいていくため、 { f'(b)-f'(a) }の部分がほぼ0になってしまいます。 そのため、この関数で、 x = 0 から x = 100とか x = 260とかまで積分すると、 (前の計算との差)が、h2よりも激しく減少するのです。 上の例では、n=256, n=512 と進むと激しく差が減っています。 次の例は、さらに計算を続けると、かえって差が増えていくことが示されています。 これは「丸め誤差」の蓄積が「打切り誤差」より大きくなってきたことを示しており、 ベストな刻み数はn=1024であることがわかるのです。 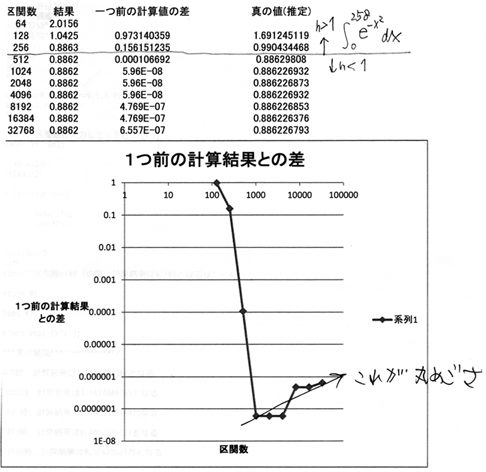
| h3が出て こない理由 |