-
$\displaystyle
\int_{x=0}^{x=1} x \, e^{3x} dx$
解答例
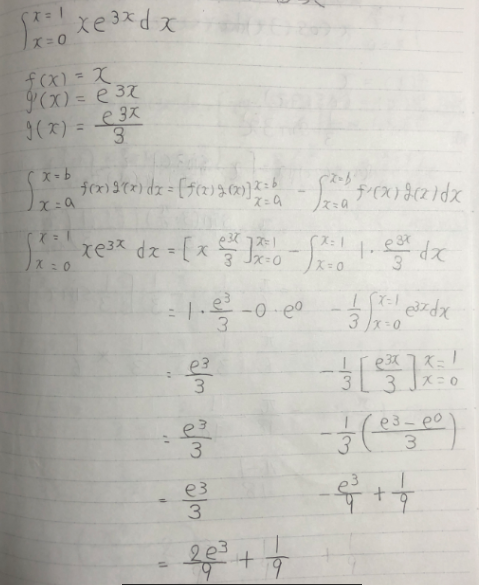
- $\displaystyle \int_{x=0}^{x={\Large \pi \over 6}} x \, \cos{(3x)} dx$
cos( )の外にある分数と、角度の中の分数を混同しないこと

積分範囲 $x=0$ を見ると、反射的に0だと思いがちですが、
$\cos 0$ や $e^0$ は0ではないので気をつけましょう。
- $\displaystyle \int_{x=0}^{x={\Large \pi \over 6}} x^2 \, \cos{(3x)} dx$
- $\displaystyle \int_{x=0}^{x={\Large \pi \over 6}} x \, \cos{(3x)} dx$
-
やってみたら 答え合わせ