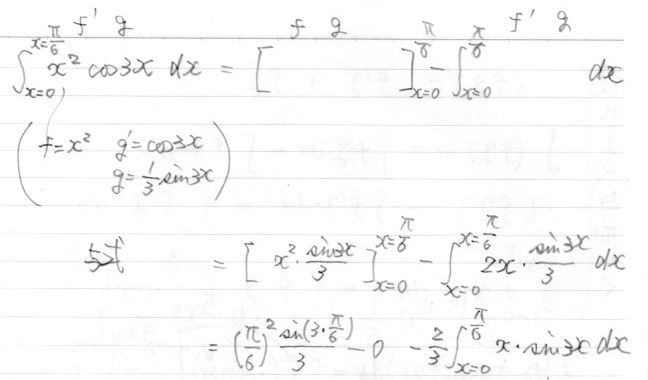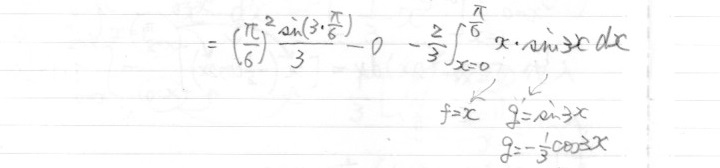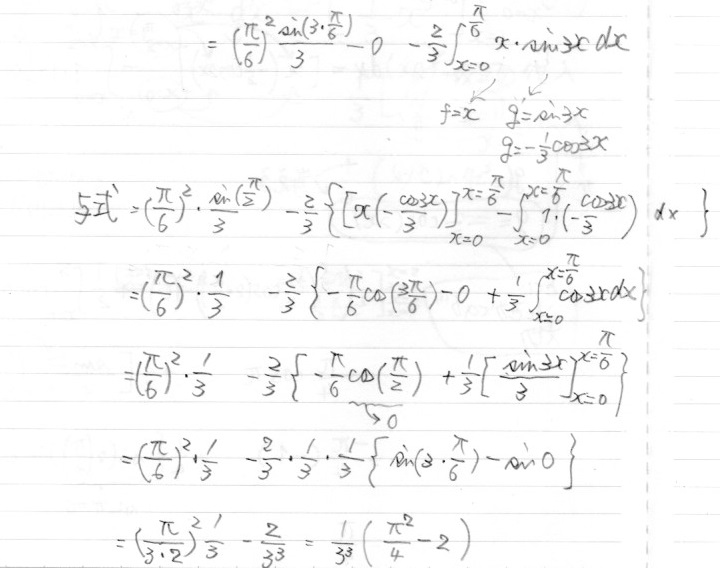1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

解析 I 定積分の部分積分

$\displaystyle \int_{x=0}^{x={\Large \pi \over 6}} x^2 \, \cos{(3x)} dx$: 最初の１回めの部分積分はだれでもしますが、

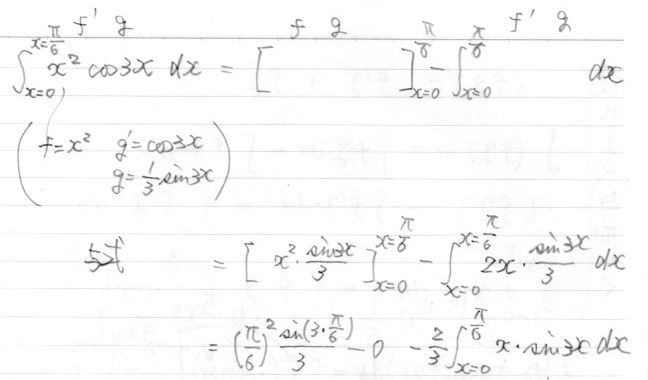
計算していくと、右辺に $x \sin{(3x)}$ の積分が出てきましたね。掛け算の積分です！

掛け算の積分だから、 $f$ を $x$ , $g'$ を $\sin{(3x)}$ と考えて、もう一度部分積分します。

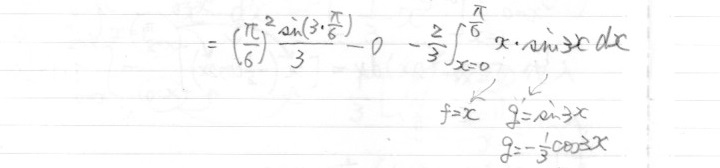
教訓：必要になったら何度でも部分積分する。

部分積分を２回やったら、当然、式は長くなっていきます。

途中で改行するなら積分の途中ではなく切りのいいところで改行する、
長くなることを見越してあらかじめ詰めて書いておく、などの対処をするといいです。

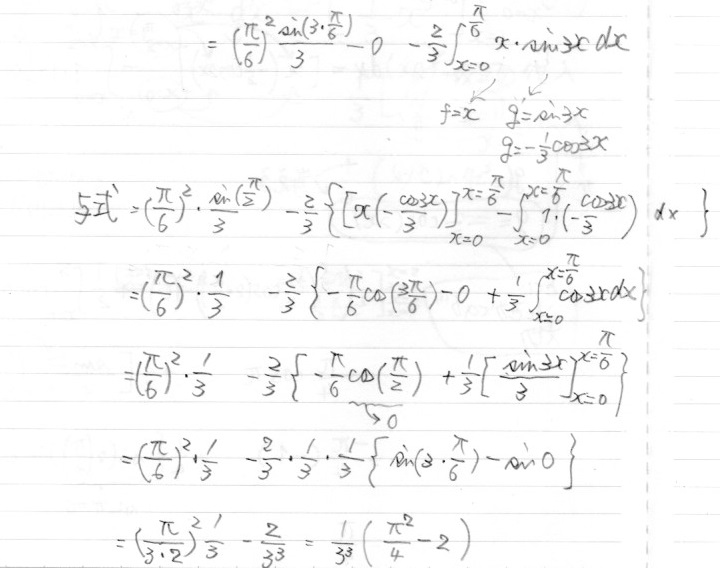
きれいに書けなかったなら、書き直してみるとよいです。答案上手に書けるようになります。
次の問題：: $\displaystyle \int_{x=0}^{x={\Large \pi \over 6}} x^2 \, \sin{(2x)} dx$

$\displaystyle \int_{x=0}^{x=1} x^2 \, e^{2x} dx$

書いたら答え合わせ

 もくじに戻る