-
一周全部あるのを「円」、
円の一部しかないのを「弧(こ)」といいますが
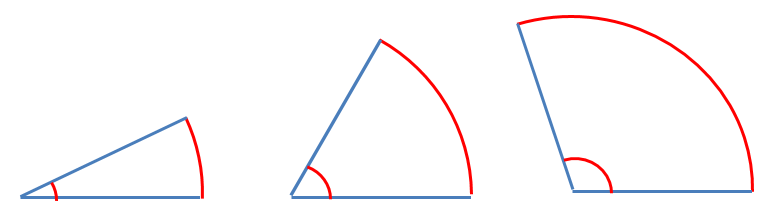
角度が小さければ弧は短く、
角度が大きければ弧は長く、
「弧」の長さは、角度に比例しますよね。
それなら、角度を表すのに、半径1の円の
「弧」の長さを使ってもよいのではないでしょうか?
- 円周の長さ
-
半径 $r$ の円周の長さは 2$\pi r$ でしたよね。
意外と忘れている人が多いので、覚え方。
この図を見ると、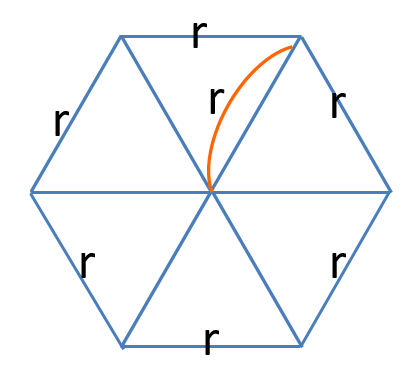
正6角形の周囲の長さは $6r$ですよね。
半径 $r$ の円周の長さは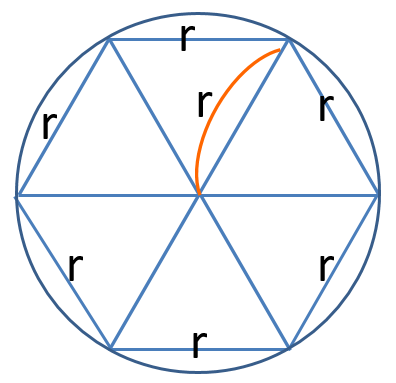
6角形の周囲の長さより少し長いですよね。
$6r $ より少し長い 2$\pi r$ が円周の長さです。($\pi =3.1415...$)
ていうか、そもそも、「円周率」の定義が
\begin{align}
円周率\pi \equiv \frac{円周の長さ}{直径(2r)}
\end{align}
なので円周の長さ$= 2 \pi r$ は当たり前なんだけど、、
当然、半径1の円周の長さは$ 2 \pi $ ですね。
-
弧度法
-
半径1の円の弧の長さで角度を表す方式です(教科書p10)。
-
1周360°の
 周の長さ $2\pi$ 周の長さ $2\pi$
これより360°のことを$2\pi$ radian(ラジアン)と呼びます。
[rad] とかいたらラジアンの略です。
角度180°の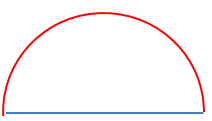 弧の長さ $\pi$ 180°は$\pi$ [rad] 弧の長さ $\pi$ 180°は$\pi$ [rad]
角度120°は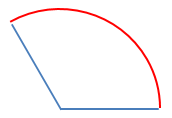 弧の長さ $\frac{2\pi}{3}$ $\frac{2\pi}{3}$[rad] 弧の長さ $\frac{2\pi}{3}$ $\frac{2\pi}{3}$[rad]
角度 90°は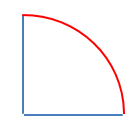 弧の長さ $\frac{\pi}{2}$ $\frac{\pi}{2}$[rad] 弧の長さ $\frac{\pi}{2}$ $\frac{\pi}{2}$[rad]
角度 60°は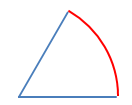 弧の長さ $\frac{\pi}{3}$ $\frac{\pi}{3}$[rad] 弧の長さ $\frac{\pi}{3}$ $\frac{\pi}{3}$[rad]
角度は教科書 p.13 にあるように、
$x$ 軸から第一象限に向かう方向に測ります。
- 練習
-
教科書p10 例題3、練習問題3をやってみて自己採点
教科書p12 例題4、練習問題4をやってみて自己採点
教科書p14 例題5、練習問題5をやってみて自己採点
次へ
|



 周の長さ $2\pi$
周の長さ $2\pi$  弧の長さ $\pi$ 180°は$\pi$ [rad]
弧の長さ $\pi$ 180°は$\pi$ [rad] 弧の長さ $\frac{2\pi}{3}$ $\frac{2\pi}{3}$[rad]
弧の長さ $\frac{2\pi}{3}$ $\frac{2\pi}{3}$[rad] 弧の長さ $\frac{\pi}{2}$ $\frac{\pi}{2}$[rad]
弧の長さ $\frac{\pi}{2}$ $\frac{\pi}{2}$[rad] 弧の長さ $\frac{\pi}{3}$ $\frac{\pi}{3}$[rad]
弧の長さ $\frac{\pi}{3}$ $\frac{\pi}{3}$[rad]