| ラプラス変換 |
|
元のページ |
「インダクタンスLのコイル、抵抗値Rの抵抗、電気容量Cのコンデンサ を電源に直列につなぎ、 時刻 t=0 にスイッチを入れた。これ以降の電流 i(t) を求めよ」 のような問題で L di(t)/dt + R i(t) + q(t)/C = E(t) をラプラス変換し微分法則 を使って dq(t)/dt = i(t) のラプラス変換を代入して ( Ls + R + 1/Cs )  ( i ) ( i ) =  ( E ) + Li(0) - q(0)/Cs ( E ) + Li(0) - q(0)/Cs この左辺に出てきた( Ls + R + 1/Cs )を 「特性関数」または「インピーダンス」 と呼んだりもしています。 この( Ls + R + 1/Cs )には、 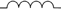 のインダクタンスL、 のインダクタンスL、 の抵抗値R、 の抵抗値R、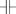 の電気容量C、 の電気容量C、という パーツの特性だけが入っています。 その一方、 初期条件i(0), q(0) とか、 どんな電源E(t)をつないだか、という条件には無関係です。 この回路の特性を表しているので、 この( Ls + R + 1/Cs )のことを 「特性関数」と呼んだりするわけですね。 |
( Ls + R + 1/Cs )は 「特性関数」 または 「インピーダンス」 |
|
|
ちなみに、
この( Ls + R + 1/Cs )の逆数のことを、 「伝達関数」とも呼びます。 なんで逆数にしただけで別の名前を付けるん?というご意見もあるかと思いますが、 名前があるということは、よく使うんだな、 ということを感じていただければと思います。 「初心者用ラプラス変換解説」最初のページへ戻る |
「伝達関数」 |