| テイラー展開 |
|
初心者向テイラー展開解説 最初のページに戻る f(x) = .... を x=a の周りでテイラー展開しなさい といったら、 (x-a)とか (x-a)2とか (x-a)3とか (x-a)4とか (x-a)5とか (x-a)6とか の式を使って f(x) 〜 c0 + c1(x-a) + c2(x-a)2 + c3(x-a)3 + c4(x-a)4 + ... の形に近似するわけですが、そもそも なぜこういう形においても良い、と仮定できるのか? とご質問をいただきました。 テイラーの定理から証明するんですが、 教科書の説明だとあまり直感的にわかりやすくはないんですよね。 思い起こせば私も高校生のとき同じ質問を先生にしましたっけ。 細かいことにはこだわらずに大雑把にわかるような説明を 書いておいたのですが、お渡しする機会が無かったので ここに載せておきます。字汚くてごめん。時間ができたら直します。 以下、x-a = h , つまり、 x = a+h と考えて読んでください。 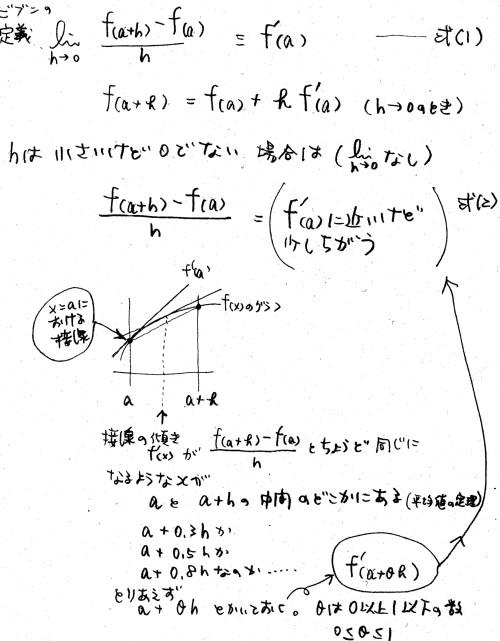 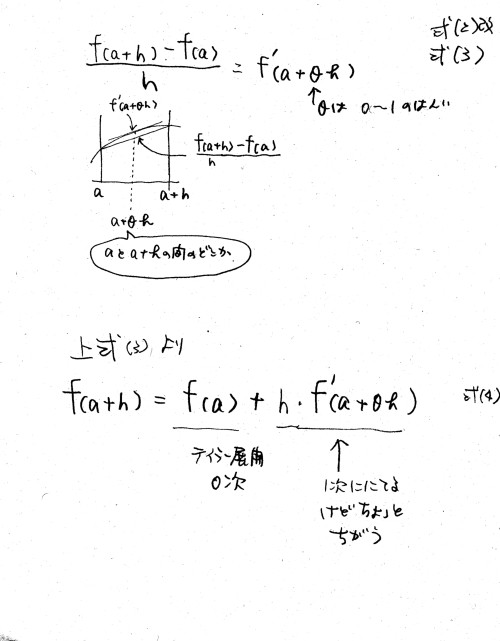 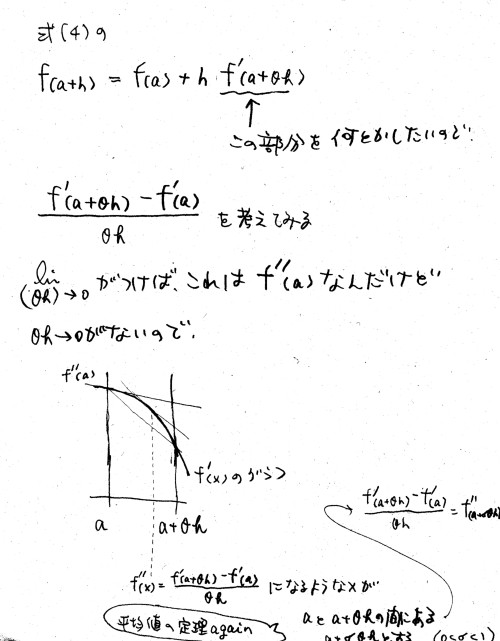   教科書にある証明はこちら。 部分積分を使った、別の面白い説明が 杜陵サークル2月定例会というページの中にありましたので ご紹介します。盛岡第三高校の下町壽男先生による 「部分積分とテーラー展開」という題の記事です。 テイラー展開解説に戻る 初心者向テイラー展開解説 最初のページに戻る 苦情、コメントはこちらへ |