▽ （ εo E ）＝電荷密度ρ＝ q ( ni - ne )

（n_i, n_eはionと電子の数密度、q =|q|は素電荷）

E= -▽φ_(r) 電位（位置rの関数）

-εo ▽2 φ(r) = q ( ni - ne )

ionは重いのでちょっとくらいポテンシャルがあっても密度変わらず
n_i = n_∞
電子は負のポテンシャルφ_(r)のところには居づらい
n_e = n_∞ exp( -q_eφ_(r)/kT_e)　 　ここで q_e=-|q|= -q とかくと
n_e = n_∞ exp( q φ_(r)/kT_e)

-εo ▽2 φ(r) = qn∞ { 1 - exp( qφ(r)/kTe) }

▽2 φ(r) = qn∞/εo { exp( qφ(r)/kTe) -1 }

qφ_(r)/kT_eを微小と思って0の周りで Taylor展開
f(x) 〜 f(0) + f'(0)x + f''(0)/2! x² + f'''(0)/3! x³ +...
exp(x) 〜 1 + x + x²/2! + x³/3! + ...
exp( qφ_(r)/kT_e)〜 1 + (qφ_(r)/kT_e) + ...

▽2 φ(r) 〜 qn∞/εo { qφ(r)/kTe }

▽2 φ(r) 〜 q2n∞/εokTe { φ(r)}

▽²はデカルト座標（普通の(x,y,z)座標）なら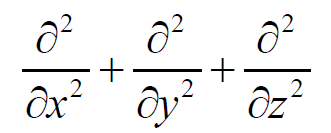

衛星のサイズがデバイ長より大きくて、衛星が壁のように見えるなら、
１次元の変化だけ考え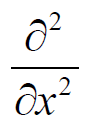
としてよい。
アンテナみたいな細長いもので、軸対称なら、円筒座標のrだけ残して

デバイ長に対して衛星が小さくて点みたいに考えてよいなら、球対称と考え

を使って積分する。

１次元ならもちろん

φ(x) = φ0 exp( -ax )

の形の解が得られ、 a²=q²n_∞/ε_okT_e

aを1/λ_Dとかくと

φ(x) = φ0 exp( -x/λD )

λ_D² = kT_e / (q²n_∞/ε_o)
λ_D² = (kT_e /m_e)/ (q²n_∞/ε_om_e)
λ_D² = (1/2)( 2kT_e /m_e)/ (q²n_∞/ε_om_e)
λ_D² = (1/2) v_the²/ω_pe²
λ_D = (1/√2) v_the/ω_pe　電子の熱速度をプラズマ角周波数で割る

衛星からこれくらい離れれば、衛星の電位が1/e になりますよという距離。
プラズマ密度n_∞が大きければ短く、電子温度T_eが高ければ長くなる。
電場を測るアンテナはこれより長くないといけないため、希薄で高温のプラズマの環境に行く衛星は とてつもなく長いアンテナを伸ばす必要がある。

戻る　 最初に戻る　

◆中川研HOME