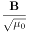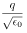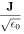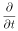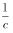| MKSAからヘビサイド・ローレンツ単位系へ |
|
前のページ まとめると |
MKSAの( 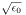 E)を
Heaviside-Lorentz系の電場EH
と考え E)を
Heaviside-Lorentz系の電場EH
と考え
MKSAの( 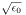 φ)が
Heaviside-Lorentz系の電位φH
になるので φ)が
Heaviside-Lorentz系の電位φH
になるのでMKSAの qかけるφ は Heaviside-Lorentz系の qHかけるφHと同じ |
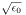 E
=EH E
=EH
|
MKSA
|
Heaviside-Lorentz
( μo εo が 出てこなくなった代わりに 光速cが入りました) |
|||||||||||||||||||
|
MKSA単位系の プラズマ周波数 ( n q2 / εo me )1/2 サイクロトロン周波数 q B / me デバイ長 ( εo kB T / q2 ne )1/2 |
Heaviside-Lorentz単位系の プラズマ周波数 ( n qH2 / me )1/2 サイクロトロン周波数 qHBH / cme デバイ長 ( kB T / qH2 ne )1/2 |
|||||||||||||||||||
| 最初に戻る |