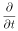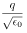東北工業大学 工学部情報通信工学科 中川研究室


ヘビサイド・ローレンツ単位系のプラズマ周波数
前のページより

Heaviside-Lorentz単位系
でのプラズマ周波数
電子の運動方程式
me d/dt ve = -qH EH
ガウスの法則
▽EH ＝ ( ni - ne) qH
連続の式
d/dt ne + ▽( ne ve )　= 0

線形化 電子密度　ne = no + ne1(r,t)
イオン密度　ni = no で線形化

運動方程式
me d/dt ve1 = -qH EH

ガウスの法則
▽EH ＝ - ne1 qH

連続の式
d/dt ne1 + no ▽ ve1 = 0

もう一度時間微分して質量を掛け
me d/dtd/dt ne1 + no ▽ ( me d/dt ve1 ) = 0

運動方程式を代入
me d/dtd/dt ne1 + no ▽ ( -qH EH ) = 0

ガウスの法則を代入
me d/dtd/dt ne1 - noqH ( -ne1 qH ) = 0

　d/dtd/dt ne1 + ( noqH2/me ) ne1 = 0

ne1 として exp( iωt ) の形の解を仮定すれば
プラズマ周波数
ωp2 = ( noqH2/me )

続く　 		単に
q/root_eps =qH
を代入しても出るよ

◆中川研HOME