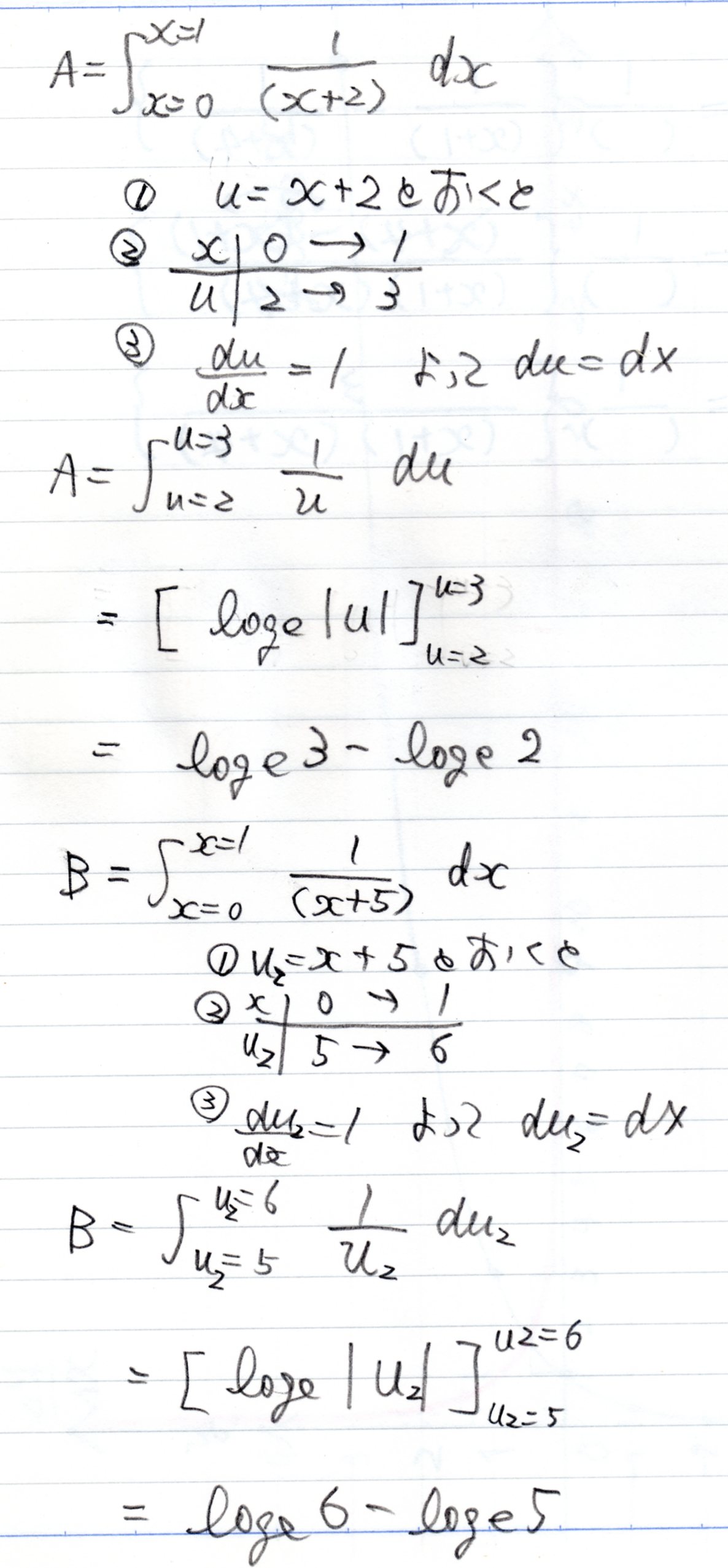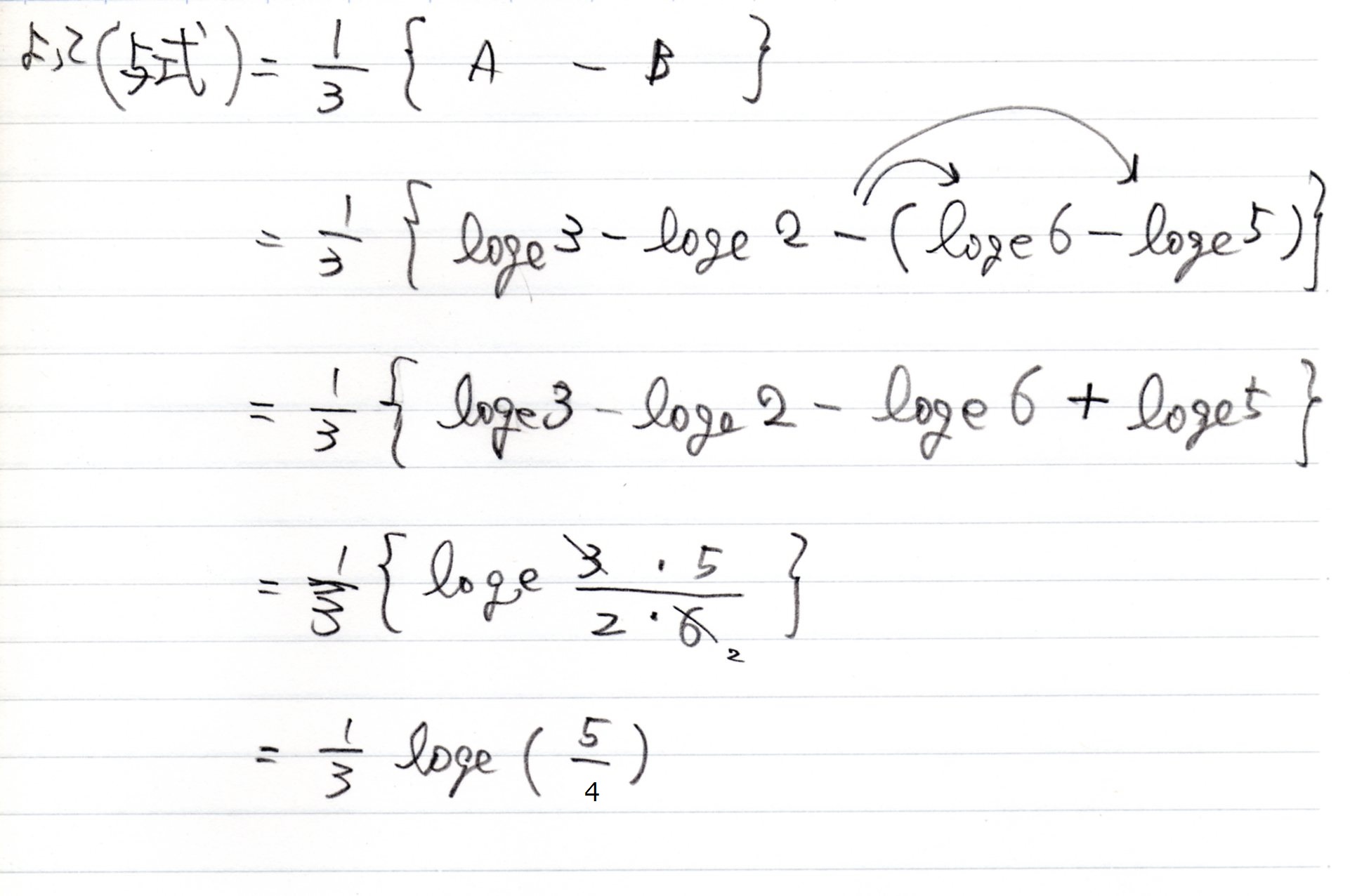部分分数分解
-
\begin{align}
\int_{x=0}^{x=1} {1 \over x^2+7x+10} \, dx
&=
\int_{x=0}^{x=1} {1 \over (x+2)(x+5)} \, dx \\
\\
&=
\int_{x=0}^{x=1}{1\over ( \qquad )} \left\{ {1 \over (x+2)} - {1\over (x+5)} \right\}\, dx
\end{align}
{ } の中を仮に通分してみると分子が3になるから、
元の式と等しくするためには ( )の中は3ですね。
だから
\begin{align}
\int_{x=0}^{x=1} {1 \over x^2+7x+10} \, dx
&=
\int_{x=0}^{x=1} {1 \over (x+2)(x+5)} \, dx \\
\\
&=
\int_{x=0}^{x=1}{1\over ( 3 )} \left\{ {1 \over (x+2)} - {1\over (x+5)} \right\}\, dx \\
\\
&=
{1\over 3} \left\{
\int_{x=0}^{x=1}{1 \over (x+2)} \, dx -
\int_{x=0}^{x=1}{1 \over (x+5)} \, dx
\right\}
\end{align}
前半を$A$, 後半を $B$ などと置いて、それぞれ求めてから最後にまとめればよいです。
例:
\begin{align}
A&=
\int_{x=0}^{x=1}{1 \over (x+2)} \, dx \\
B&=
\int_{x=0}^{x=1}{1 \over (x+5)} \, dx \\
とおくと\\
(与式)&=
{1\over 3} \left\{ A-B \right\}\\
\end{align}
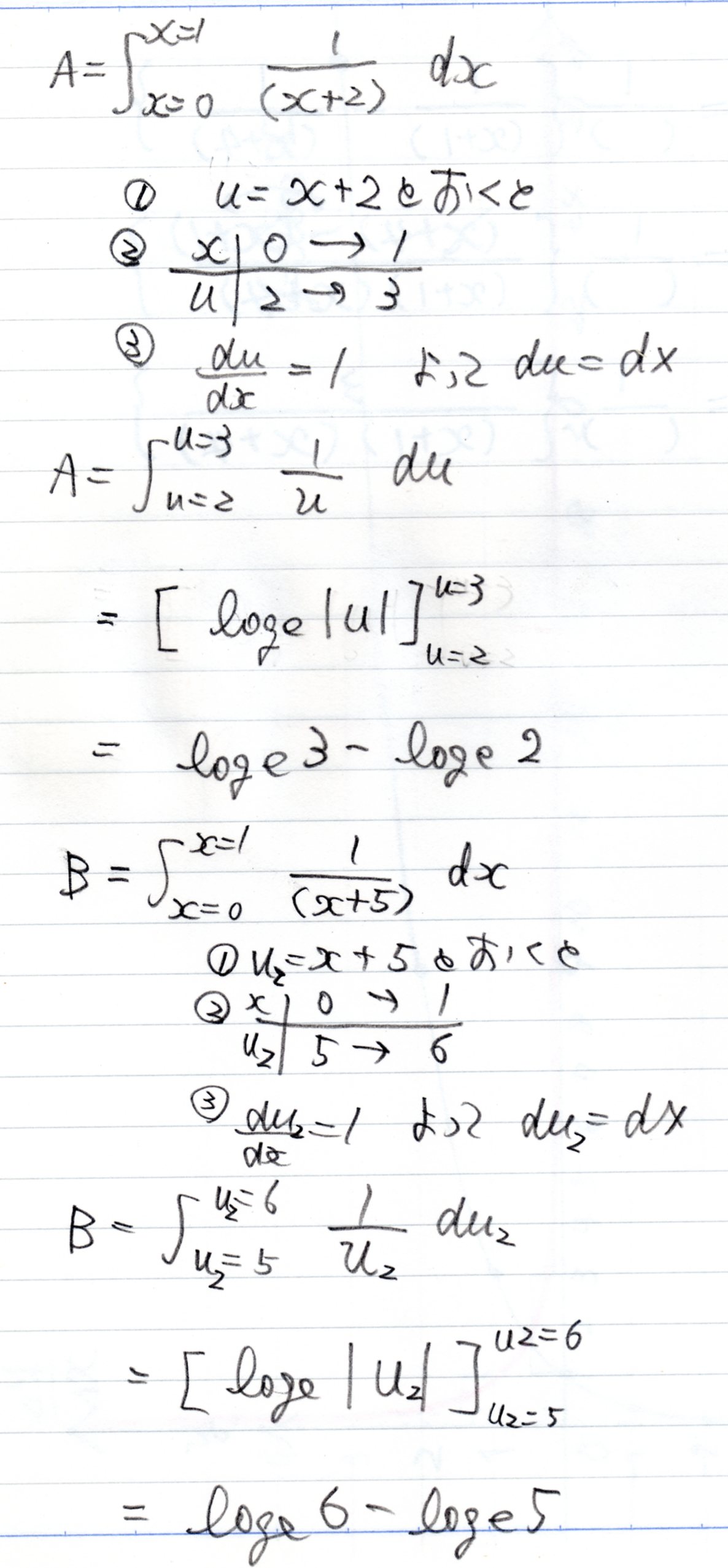
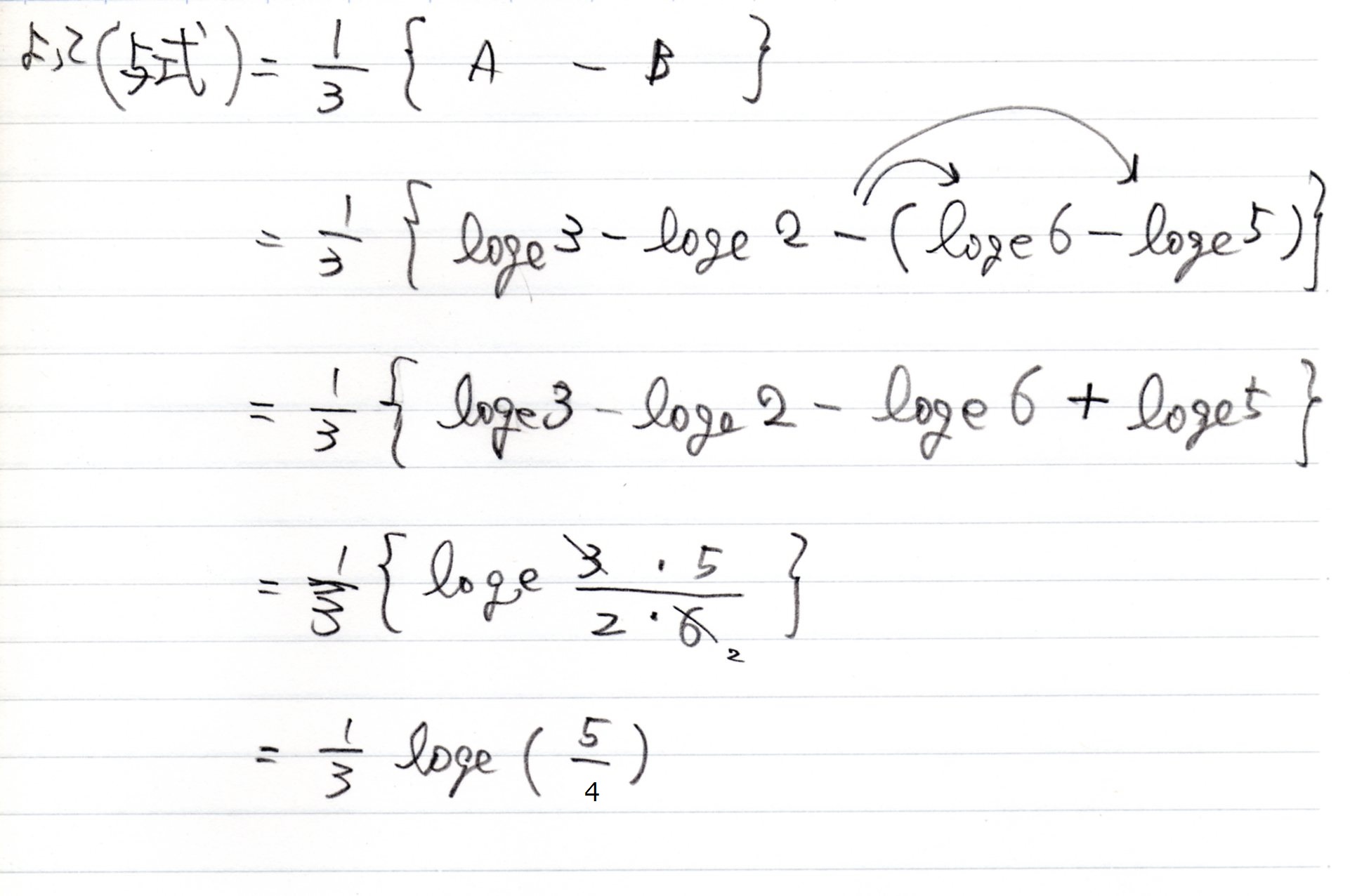
別解
\begin{align}
\int_{x=0}^{x=1} {1 \over x^2+7x+10} \, dx
&=
\int_{x=0}^{x=1} {1 \over (x+2)(x+5)} \, dx \\
\\
&=
\int_{x=0}^{x=1}{1\over ( 3 )} \left\{ {1 \over (x+2)} - {1\over (x+5)} \right\}\, dx \\
\\
&=
{1\over 3} \left\{
\int_{x=0}^{x=1}{1 \over (x+2)} \, dx -
\int_{x=0}^{x=1}{1 \over (x+5)} \, dx
\right\} \\
\\
&=
{1\over 3} \Bigl[ \quad
\log_e|x+2|- \quad
\log_e|x+5| \quad
\Bigr]_{x=0}^{x=1}\\
\\
&=
{1\over 3} \left\{
\log_e|1+2|- \log_e|1+5| - (\log_e|0+2|- \log_e|0+5| )
\right\} \\
\\
&=
{1\over 3} \left\{
\log_e|1+2|- \log_e|1+5| - \log_e|0+2|+ \log_e|0+5|
\right\} \\
\\
&=
{1\over 3} \left\{
\log_e{ 3 \cdot 5 \over 6 \cdot 2 }
\right\} \\
\\
&=
{1\over 3} \left\{
\log_e{ 5 \over 4 }
\right\} \\
\end{align}
- 練習
-
教科書p.101 練習42 (1)(2)
次のページ
|