| 分散関係式(ω-k ダイヤグラム) |
|
前のページ |
ω-k図をかこうとしたときに困りがちなポイントは2つ、 ・横軸がkだからといってkからωを求めようとすると無駄に大変 ・リアルな値を入れようとするとはみ出してかけない |
||||||||||||||||||||||||||||||||||||||||||||
| ωからkを |
発想を転換して、ωから k を求めてグラフを書けば簡単です。
「cold近似平衡伝搬」の右回りの式
右辺のωに数値を代入すればkが計算できますね。 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
電磁波の分 |
また、右辺がパーツに分かれているところもよい点で、 もしイオンも電子もない真空中ならば、 ωpi = 0 , ωpe = 0 なので 単に k2c2 = ω2 となります。 これは学校で習った真空中の電磁波の伝搬の式です。 ω/k = Vphを使えば Vph = +-c とも書けるし、 k = 2π/λ,ω= 2πf を使えば c = +- fλ とかくこともできます。 |
k = 2π/波長λ ω= 2π/周期T 周波数 f = 1/T ω= 2πf Vph = ω/k (位相速度) |
|||||||||||||||||||||||||||||||||||||||||||
| イオンの分 |
赤で書いたイオンの所を、分子のωがなくなるようにちょこっと変形し
|
双曲線
x = -b, y = a |
|||||||||||||||||||||||||||||||||||||||||||
|
パーツ別 グラフ |
縦軸 y を k2c2 とし、横軸をωとして 電磁波の分 y = ω2 を緑で、 イオンの分の双曲線をピンクで書くとこんな感じ 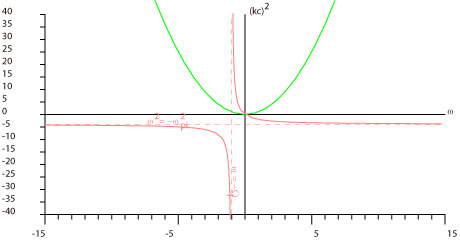
|
||||||||||||||||||||||||||||||||||||||||||||
| 電子の分 |
青で書いた電子の所も変形すると
電子の分は 漸近線 ω = Ωe と y = - ωpe2 の双曲線になります。 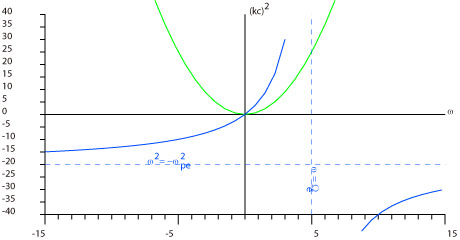
|
||||||||||||||||||||||||||||||||||||||||||||
|
イラストっぽく描く |
リアルに描こうとすると、 電子サイクロトロン角周波数Ωeと イオンサイクロトロン角周波数Ωiの桁が違いすぎて、 Ωpiが入るように書くとΩeがはみだし、 Ωpeが入るように書くとΩiがつぶれて見えなくなり 結構困ります。 教科書とか先生の板書のように イラストっぽく描くためには、 リアルな数値はいったんあきらめて 1枚のグラフに入るような数値を選んで書くとよいです。 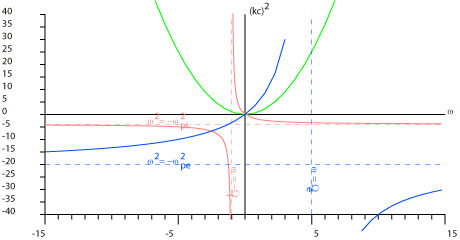
|
リアル Ωi: Ωe = ωpi2: ωpe2 = 1 : 1836 左の作図用 Ωi: Ωe = 1 : 5 リアル Ωi : ωpi = VA : c = 1 : 数千 (太陽風中) 左の作図用 Ωi : ωpi = 1 : 2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
続く
|
||||||||||||||||||||||||||||||||||||||||||||