| 分散関係式(ω-k ダイヤグラム) |
|
前のページ とりあえず 縦軸k2c2の グラフ |
cold近似、平衡伝搬、n2 = R の分散関係式を
パーツごとに計算したものを、ぜんぶ足したのが黒い線です。 これならExcelとかでもできます。 | |||||||||||||
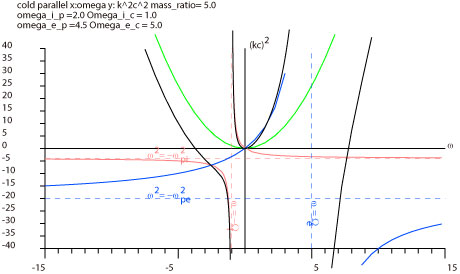
このグラフの縦軸はまだk2c2のままなのですが、 この段階でもわかることがあります。 外側の黒い線2本は、上の方(kが大きい方)に行くと、緑色の線(電磁波の線)に近づいていきそうです。 縦軸に近い方の左(ω<0)の曲線は、イオンの赤い線に近いです。 縦軸に近い方の右(ω>0)の曲線は、電子の青い線に近いです。 |
多成分も できます |
|||||||||||||
|
縦軸を kc に |
k2c2は、2乗してるのだからプラスのはずで、 このグラフの下半分には用はないです。 k2c2がプラスとなっているところだけについて その平方根を求めて 縦軸が| kc | のグラフに書き直したのがこれです。 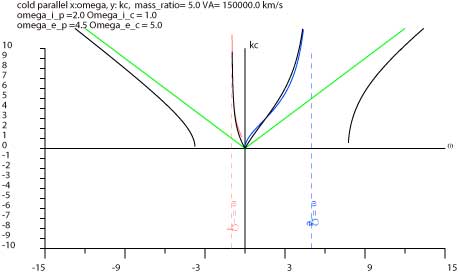
電磁波の緑の線は、新しいグラフでは直線になりました。 平方根は、kがマイナスの解もあるので、k<0 側にも折り返し、 スケールを消して 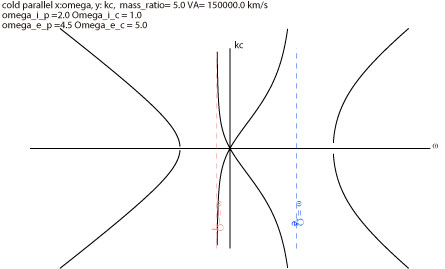
縦横ひっくり返せばできあがり 上半分 ω>0 が右回り、下半分 ω<0 が左回り 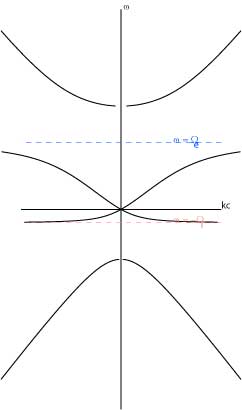
イラストっぽく、右回り左回りを1枚に描くために、 イオンと電子の質量比をリアルの値よりも小さくしてあります。 リアルに描くと |
|||||||||||||