| 分散関係式(ω-k ダイヤグラム) |
|
前のページ ω-k 図 |
cold近似、平衡伝搬、n2 = R の分散関係式
イラストっぽくかいたのが左、 平均的な太陽風中のリアルな値で書いたのが右 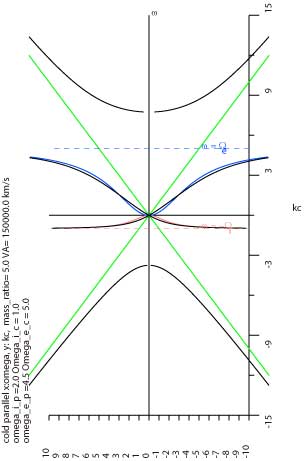
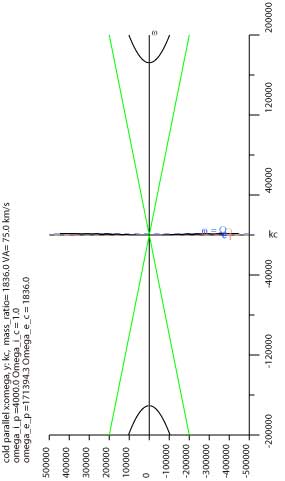
アッパーハイブリッドが入るように書こうとすると、 電子サイクロトロン周波数もホイッスラー波もつぶれて見えない。 同じパラメタで、 アッパーハイブリッドはあきらめて、ホイッスラー波が見えるスケールで書いたのが右。 ホイッスラー波の曲線の形が見えるように書こうとすると、 緑色の電磁波はほとんど軸にくっついてしまう。 イオンサイクロトロン波もつぶれて見えない。 
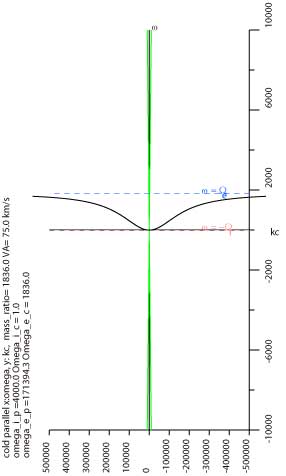
上図右のリアルに描いた図では、 青い電子の分の線と全部足して描いた黒の線がほとんど重なっています。つまり、 ホイッスラーのグラフをかくときは、電磁波の緑の線とかイオンのピンクの線分の計算は 省略してもかまわないことが分かります。ただし、この周波数、この波数のあたりでは。 同じパラメタで、 ホイッスラー波の曲線の全貌はあきらめて、 イオンサイクロトロン周波数が見えるスケールで書いたのが右。 上の図の原点付近の拡大図と思ってください。 
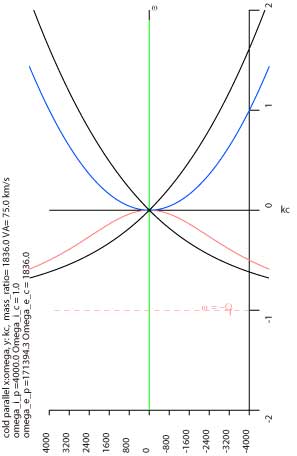
イオンサイクロトロン周波数より低い(0に近い)周波数帯では、 イオンサイクロトロンの波は、イオンのピンク色の線よりだいぶずれているし 電子サイクロトロンの波も、電子の青い線とはだいぶ違っています。 黒い線は、ωが0に近づいていくと、 傾きがアルフベン速度 V A、または -V A の直線に近づいていきます。 だからVLFの本見てホイッスラー波の式をとってきて低周波に使っちゃダメってことです。(自分へのつっこみ) 低周波なら単に傾き V A と -V A の直線かいたほうがましです。 こんな低周波の波を磁気流体波(Magneto Hydro Dynamic, 略してMHD波)といいます。 ω<0(左回り)のイオンサイクロトロンの低周波のとこをアルフベン波、 ω>0(右回り)の電子サイクロトロン波(ホイスラー波)の低周波のとこをモディファイド アルフベン波、 といいます。 もともとMHD出身だとどちらも気にせずアルフベン波、と言っちゃって、 プラズマ波動できる人に嫌がられたりしていました。 |
||||||||||||
| 使用した値
|
上図で使ったパラメタは 左のイラスト用が Ωi : Ωe = 1 : 5 および Ωi : ωpi = 1 : 2 右のリアル太陽風が Ωi : Ωe = me : m i = 1 : 1836 および Ωi : ωpi = V A : c = 75 km/s : 3×105 km/s (恒等式) でした |