| 分散関係式(ω-k ダイヤグラム) |
|
前のページ |
イオンと電子の2成分のプラズマ(cold 近似、平行伝搬)の分散関係式
縦軸を k2c2としたグラフをかくとこんなかんじ。 黒いのがすべてを足した線。 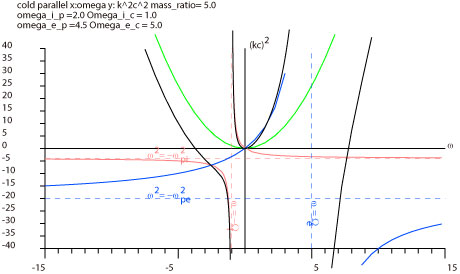
それぞれの成分のサイクロトロン周波数のところで一回切れます。 ω = -Ωiの近くではイオンの分のグラフに近く、 ω = Ωeの近くでは、電子の分のグラフに近いです。 |
||||||||||||||||||||||
|
多成分もできます |
イオンが1種類でなく、もっと重いイオンも交じっているようなときは、 重いイオンの双曲線も付け加わり
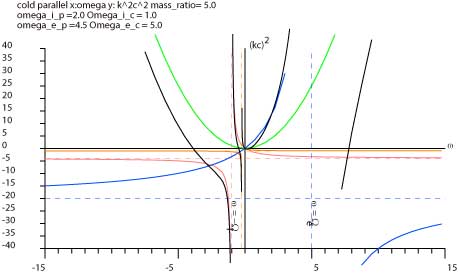
新しい重いイオンのサイクロトロン周波数ω= -Ωjのところでさらに線が切れていきます。 イオンの種類が増えれば増えただけ、 分母が0になるところで分岐が増えていきます。 イオンが増えてできる分岐はω<0 側(左回り)の領域だけにあります。 |
||||||||||||||||||||||
|
| |||||||||||||||||||||||
|
|