| 分散関係式(ω-k ダイヤグラム) |
|
プラズマ波動の分散関係式 (ω-k ダイヤグラム)を イラストっぽく描く 東北工業大学 情報通信工学科 中川朋子 |
|||||||||||||||||||||||||||||||||||||||||||
| 分散関係式 |
プラズマ波動の教科書なんかに出てくる分散関係式。 プラズマ中に存在できる波の周期Tと波長λの条件を 波数 k( = 2π/波長λ)と 角周波数 ω(= 2π/周期T)を使って書いたものです。 一番簡単な場合「cold近似平衡伝搬」の右回りの式は
教科書などではよく、左辺の
また、 角周波数ωを波数kで割ると 波の位相速度 Vphになるので、
|
左回りは? Ωi イオンサイクロトロン 角周波数 ωpi イオンプラズマ角周波数 Ωe 電子サイクロトロン角周波数 ωpe 電子プラズマ角周波数 n = ck/ω 屈折率 Vph = ω/k 位相速度 それなら屈折率は n = c / Vph |
|||||||||||||||||||||||||||||||||||||||||
| 分散曲線 |
これらの式のグラフをかいたものが分散曲線です。 最後の式を使えば、角周波数ωから位相速度 Vphを求めることができるので、 横軸がω、縦軸が位相速度 Vphというグラフがかけます。 周波数ごとに、速度がどう違うのかがわかって便利です。 |
ω-V図、f-V図 |
|||||||||||||||||||||||||||||||||||||||||
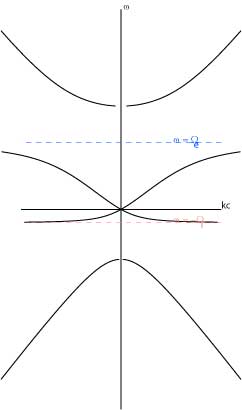
| ω-k図 |
最初の式を使うと、
横軸に波数k、
縦軸に角周波数ω をとったグラフがかけます。 ω-k ダイヤグラムと呼んだりもします。 ω-k 図を使うと、 曲線上の点(k,ω)と 原点を結んだ直線の傾き ω/k が位相速度、 その点での接線の傾き dω/dk が群速度となり、 ドップラー効果によって周波数が変わってみえることも 直線でかけるので、 人工衛星で観測された電場や磁場の変動を説明するときなどに便利です。 でも実際に描こうとすると、 結構困ります。 続く |
|