| 離散フーリエ変換(DFT) |
| スペクトル |
横軸が周波数、縦軸がパワー a2+b2、または 横軸が周波数、縦軸が振幅 √(a2+b2) のグラフのことをスペクトルといいます。 |
| スペクトルの横軸 |
m=1, 2, 3, ... は、 T秒間にそれぞれ1個、2個、3個 波が入るのですから、 周期はそれぞれ T, T/2, T/3, ....ですよね。 周波数 f は周期T の逆数なのですから、それぞれ f = 1/T, 2/T, 3/T, .. .になります。 T = d秒間隔,N個のデータなら m = 0 周期 = ∞ 周波数f = 0 m = 1 周期 = T 周波数f = 1/T = 1/(Nd) m = 2 周期 = T/2 周波数f = 2/T = 2/(Nd) m = 3 周期 = T/3 周波数f = 3/T = 3/(Nd) m = 4 周期 = T/4 周波数f = 4/T = 4/(Nd) : : つまり 周期 = T/m 周波数 = m/T = m/(Nd) : : これが横軸。番号mと全体の個数Nとサンプリング間隔dが分かれば、 m番の波の周波数がわかるわけだ。 問題文にサンプリング間隔dが書いてないときは、 サンプリング間隔dとおいて m番の周波数は m/(Nd) = (m/N) (1/d) サンプリング間隔d の逆数(1/d) は、 1秒間に何個データを取っているか(サンプリングしたか)を表しますよね。 これをサンプリング周波数と言います。 これを f0 と定義すれば m番の周波数は (m/N) (1/d) = (m/N) f0 [Hz] たとえばN = 8 個なら m = 1 周期 = 8d 秒 周波数f = 1/(8d) = 0.125 f0 Hz m = 2 周期 = 8d/2 秒 周波数f = 2/(8d) = 0.250 f0 Hz m = 3 周期 = 8d/3 秒 周波数f = 3/(8d) = 0.375 f0 Hz : : グラフに書くときは、 横軸に0, 1, 2, 3,...みたいに書いて、 単位のところに [×0.125 f0 Hz] ( f0はサンプリング周波数)のように書くか、 横軸に0, 0.125, 0.25, 0.375 ,...みたいに書いて、 単位のところに [× f0 Hz] ( f0はサンプリング周波数)のように書くとよいです。 |
| スペクトルの縦軸 |
縦軸に振幅、というと、いきなりamとかbmを書く人がいますが、
それじゃあまり意味がないです。 sin x の波形でも、測定開始が少し遅れれば、cos x の波形になってしまいます。 同じ波の振幅が、測定開始の時刻によって、bmになったりamになったりしちゃうわけです。 グラフがamとbmの2枚に分かれちゃうのも使いづらいですよね。 フーリエ級数展開 f(x)〜a0 + a1 cos(2px/T) + a2 cos(4px/T) + a3 cos(6px/T) + ... + am cos(2pmx/T) + ... + b1 sin(2px/T) + b2 sin(4px/T) + b3 sin(6px/T) + ... + bm sin(2pmx/T) + ... に出てくる a1 cos(2px/T) と b1 sin(2px/T) は どちらも周期 T の波ですし、 am cos(2pmx/T) と bm sin(2pmx/T) は、どちらも周期 T/m の波です。 同じ周期の波の足し算 am cos(2pmx/T) + bm sin(2pmx/T) は、まとめて Am cos(2pmx/T + φ) の形にも書けますよね (三角関数の位相表示 ) 振幅 Amは Am2 = am2 + bm2 で求められます。 Am = √( am2 + bm2 ) これを使えば、どんな周波数(周期)の波が強いのか、一目でわかるグラフ(=スペクトル)ができます。 Amは2乗の和の√ですから、縦軸はマイナスになりません。 振幅Amの2乗はパワーですから、√を取らずにそのまま使えばパワーのスペクトルになります。 Power = Am2 = am2 + bm2 |
| グラフの種類を選ぶ時 |
スペクトルの横軸(周波数 f ) は、どんな種類の波か、ということを表しています。
光だったら、 4×1014 Hz くらいだったら赤色、 6-7×1014 Hz くらいだったら青色、みたいに、 周波数が光の種類を表します。 違う種類のものを比べるときは、なるべく、棒グラフを使いましょう。 良い例 良くない例 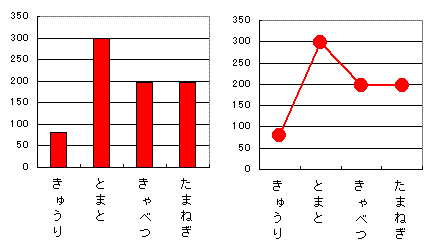 左のグラフは普通だけど、右はなんか変ですよね。 とまとが最後に来たって別にいいわけだし 一方、同じものの時間変化を追跡していくときは、折れ線グラフ( Excelなら「散布図」)がいいです。
|
||
| 波形と呼ばないで |
レポートの考察などで、スペクトルのグラフの形について書くとき、「波形」と書く人がいますが、 「波形」は、元の、横軸が時間のときのグラフにのみ使ってください。 じゃあスペクトルのグラフはなんて書く? 「スペクトルの形」でお願いします。 |
||
|
|
課題に戻る |