情報通信工学科 コンピュータ数値解析(学内専用）担当：中川朋子


オイラー法によるシミュレーション
----------- 出力のヒント ----------

・計算結果だけでなく、時刻も出力しよう
printf("%f\n", y); だけでなく、
時刻t= 回数kaisu * 時間刻みdt も計算しておいて、並べて出力させる
printf("%f ", t); ←時刻。あえて改行の \n を入れないことによって１行に並ぶ
printf("%f ", v); ←速度。あえて改行の \n を入れない。次の数字とくっつかないよう最後に空白
printf("%f\n", y); ←位置。最後だけ改行の\nを入れる。ここまでが１行となる。
のようにすれば、時刻、速度、位置が１行に並んで出てきます。

----------- グラフを描く場合の注意 ----------

・グラフは正確に書く
縦軸、横軸に軸名（時間とか電荷とかの物理量）を記していない、数値と軸名があわない
軸の目盛りに数値を添えていない、 数値がずれている、初期条件から始まっていない

・EXELでグラフを描くなら、 折れ線グラフではなく、「散布図」を使う。
（x軸が時刻、ｙ軸が電流とか位置とかになるようにする）
普通の線グラフを選ぶと、時刻が０からでなく 1から始まってしまう

・時間刻みdtの違うグラフを重ねて書いたらずれちゃってる
刻みを変えるととんでもなくずれてしまうとか、、、
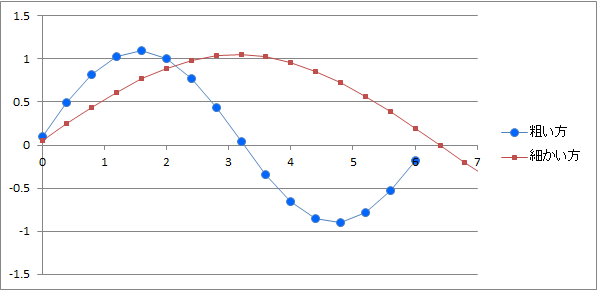
よい例 Excelでdt の異なるグラフを重ねて書く(成功) 　ダメな例 Excelでdt の異なるグラフを重ねて書く(失敗）
　　　　　　　　　　　　　　　→ｘ軸の時刻を正しく選ぶと直せる

・gnuplot でグラフをかくときはうしろにwith lp をつけると点を線でつないでくれる
例：gnuplot> plot "kekka.txt" with lp

・理論値も同じグラフに重ねて描くとなお良い
gnuplotでいきなり式を書いてもいいけど
プログラミングの段階でラプラス変換で求めた式を関数に仕込んでおいて並べて出力すると便利

・1.0と1.000000は意味が違う
縦軸や横軸の目盛りに1.0と書くところを1.00000000と書いたなら、
「小数以下８桁まで精度がある」と主張していることになります。そんなに精度ある？

----------- 提出物の書き方 ----------

１．レポートの最初に解くべき微分方程式（２本あるはず）を書く
　（このとき、最初から数字を代入してはいけません。）

２．次に、手計算で得た理論式と振動周期を書いて、時間刻みdtをいくつに設定したか書く
　手計算の途中経過（ラプラス変換）はここには書きません。
　途中計算をつけたい人は、最後のページに「付録」としてつけます。

３．使用したプログラムを添付し

４．結果のグラフ（横軸が時間、縦軸が物理量）を載せる

　出力結果（数字）をレポートにつけてはいけません。時間刻みを細かくしたら出力結果は膨大になりますね。
　レポートは「読んでもらうため」に書くので、読んでもらう必要のない数字の羅列は載せません。
　数字を見たってよくわからないから、一目でわかるように、グラフにしたのです。

５．グラフを載せたら、グラフからわかること（検討考察）を文章で書く

６．手計算の途中経過（ラプラス変換）をつける人は、「付録」として最後のページにつけます
　このときも、微分方程式に最初から数字を代入してはいけません。
　書けるところまでは物理量（ｍとかｋとか）で書いて、場合分けが必要になるところから数値を代入して解きます。

---------- 検討考察のポイント ----------------

・シミュレーション結果の振動周期や減衰の速さや振幅は、理論値と比べてどう違うか
　一見もっともらしい減衰振動のように見えても、理論値と比べると振幅や周期がちがってたりしますね。

・時間刻みdt 細かくしたらどうなっていくか
　オイラー法なら、刻みを半分にすると誤差が半分(刻みを1/10にしたら誤差が1/10)になっていくはず
　改良オイラー法なら、刻みを半分にすると誤差が1/4(刻みを1/10にしたら誤差が1/100)になっていくはず
　理論値が求められなかった人も、振幅が極大となるところの値の「差」を比較すれば書ける
　わざと「粗いdt」「普通のdt」「細かいdt」をやってみると考察書きやすいかも

・時間刻みdt は細かくすればするほど正しいのか

・シミュレーション結果は小数以下何桁まで正しいか、または真の値の何％の誤差があるか

----------- 出力のヒント その２ （出力が膨大で困るとき）----------

・dtをすごく細かくしたとき、計算1回ごとに出力していたのでは行数が膨大になって大変ですね。
　そんなときは計算回数が10の倍数になったら出力、のように、出力を間引くといいですよ。
例：
if( kaisu%2 == 0 ){ printf("%f %f %f\n", time, y, v); }　
　　　　↑　　　　　　　　　　　　　
　(kaisuを2で割った余りが0なら){ 出力 }

 オイラー法のページに戻る