| 月のウェイク境界からのホイッスラー波 |
-
月のウェイク境界からのホイッスラー波
- 中川朋子(東北工大),飯島雅英(東北大)
第11回SGEPSS波動分科会(平成18年6月9日)九州大学西新プラザ
月の裏側には,太陽風が月によって吸着されるため,ウェイクと呼ばれる低密度の領域が形成される。月ウェイクはExplorer衛星(Lyon et al., 1967; Ness and Shatten, 1969) やWIND衛星(Owen et al., 1996; Ogilvie et al., 1996, Farrell et al., 1996),Lunar Prospector衛星(Lin et al., 1998)によって直接観測されているが,ウェイクと太陽風プラズマの境界には,イオンと電子の熱速度の違いによって電荷の不均衡が生じ,電場が形成されると言われている。
この電場と深い関係があると考えられるULF波がGEOTAIL衛星によって観測されている。月から約4万7千km上流において,磁力線がGEOTAIL衛星と月の夜側を結ぶ配置となった1994年10月25日,月のウェイク起源と見られる 0.3-1.1[Hz]のULF波動が16:20-17:10と18:55から19:02の2度にわたり観測された(Nakagawa et al., 2003)。いずれもおよそ1.1 [Hz]に周波数の上限を持ち,GEOTAIL衛星では磁場に対し左回りの波として観測され,磁力線にほぼ平行に伝搬していた。この波は,太陽風より僅かに速い群速度で太陽風を遡るホイッスラー波であった。ホイッスラー波の偏波は背景磁場に対して右回りであるが,低い周波数帯では,太陽風速より僅かに遅い位相速度の為に,媒質である太陽風に対し相対的に動いているGEOTAIL衛星から見ると,ドップラー効果のために回転方向が逆周りに見えたのである。このようなホイッスラー波としては,地球前面衝撃波に起源をもつ現象 (Fairfield, 1974)が知られており,実際,この数日間も衛星は衝撃波の前面にあったが,磁力線がGEOTAIL衛星と月の夜側を結ぶ配置となったこの10月25日にのみこのようなULF波観測されたことから,この現象は月のウェイクに関連したものと考えられる。
ではこのホイッスラー波はどのようにして励起されたのだろうか。月のウェイク境界の電場によって電子が反射されることが報告されているので(Futaana et al., 2001),この反射電子との共鳴がまず考えられるが,実はこれではGEOTAILの観測したホイッスラーとは波の回転方向が合わない。サイクロトロン共鳴するためには,電子から見た電場が,電子のサイクロトロン運動と同じ向きに回転する必要があるが,この波(太陽風に乗った系でみて右回り)はGEOTAILの系から見てすでにドップラーシフトのため周波数が負となって回転方向が反転しており,さらに太陽方向に進む反射電子から見ると,周波数は下がる一方で,波は左回りにしか見えない。つまり反射電子から見た波の回転は電子のサイクロトロン運動とは逆方向となってしまいサイクロトロン共鳴を起すことができない。
逆に,電子流が反太陽方向に流れていれば,この電子から見て,速度Vswの太陽風中を進む周波数ωの波の見かけの角周波数はω-|kVsw|+|kVb|となり,これが電子サイクロトロン角周波数Ωeの整数倍になればサイクロトロン共鳴を起すことができる。ビーム速度Vbは太陽風速と位相速度の差を超えれば良いのでこれは容易に達せられる。以上により,ホイッスラー波を励起したのは反射電子ではなく,ウェイク境界の電位差より大きな運動エネルギーをもって境界を透過した電子ではないかと考えられる。「整数倍」を「1倍」とし,実際に波が観測された時刻のプラズマパラメタに応じたホイッスラーの分散曲線上で,観測された周波数の下限ωobs =0.3[Hz]を用いてサイクロトロン共鳴条件ω- |kVsw| +|kVb| = Ωeを満たす波を考えるとω=2.3×10-2Ωe (k=15.7Ωe/c) となり,この周波数で共鳴する電子のエネルギーは0.96[keV]となった(Nakagawa et al., 2003)。この電子の起源は,太陽風磁場の磁力線に沿って流れている電子のstrahl成分(1-2keV)と考えられる。
ウェイク境界を通過できた電子が,磁力線に並行に伝搬するホイッスラー波を励起するためには,共鳴条件を満たすだけでなく,十分大きな「磁力線に垂直な速度成分」を持っている必要がある。共鳴電子は,波の系から見て等エネルギー軌道に沿って動くが,磁力線に平行な速度からスタートすると粒子の系から見たときエネルギーが増えてしまい,波を励起することが出来ない。波にエネルギーを渡すためには,十分大きな「磁力線に垂直な速度成分」のある位置からスタートする必要がある。太陽風電子のstrahl成分は磁力線に沿って流れているが,月ウェイク境界の電場によってピッチ角散乱を受ければ,ホイッスラー波を励起するのに必要な「磁力線に垂直な速度成分」が得られると予想される (Nakagawa and Iizima, 2005)。
そこで本研究では,月ウェイク境界の電場構造を図1のようにモデル化し,磁力線に沿って入射したテスト粒子の軌道を追跡し,通過する電子ビームがピッチ角散乱を受けることを確かめた。ウェイク境界の電子とイオンの熱速度の違いのために電子が過剰な領域ができ,そのためにウェイク内の電位が下がり,境界面に内向きの電場が生じている。磁力線は,GEOTAIL観測と同様,ウェイク境界面に対し20度で交差させてある。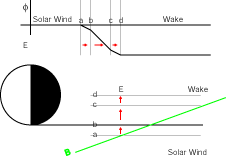
- 中川朋子(東北工大),飯島雅英(東北大)
- 図1 月ウェイク境界の(上)ポテンシャル(下)電場(矢印で表示)構造の単純化したモデル。磁場とウェイク境界面とは20度の角度で交差させてある。
- 図2 ウェイク境界電場層における電子軌道計算例。左の2枚は速度空間,右の2枚は実空間。電場層の厚さは全体で uD/Ωeの4倍としてある。左端の図(v⊥-v⊥空間)で電子はドリフト速度(uD,0)を中心に回転する。電場層に入射した時のv//はドリフト速度の4倍,v⊥は0,電場層を抜けた時にはv//はドリフト速度の約2倍,v⊥も約2倍となっている。
- 図3 さまざまなエネルギー(ドリフト速度の0-5倍)とピッチ角(磁力線に対し10度以内)で入射した電子(左),電場層で反射された電子(中),および電場層を通過した電子(右)の速度分布。
-
図4 磁場y成分の変動。横軸は時間(単位ωp−1),縦軸は距離(cωp−1)。
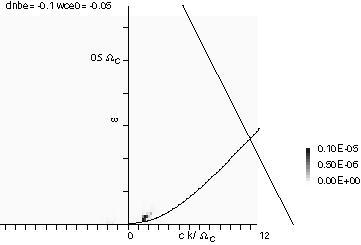
(a) Ωe/ωp= 1×10-2 (b) Ωe/ωp= 3×10-2 (c) Ωe/ωp= 5×10-2 の場合。 - 図5 Ωe/ωp = 5×10-2の場合の磁場y成分 (図4(c)) のω-kダイアグラム。 曲線はホイッスラー波の分散曲線(但しリングビームを仮定しない場合), 右下がりの直線がサイクロトロン共鳴を表す。
図2に電子軌道の追跡例を示す。この例では,初速度は磁力線に平行であったが,電場層に入ると,磁力線に垂直な電場成分の存在により,磁力線に垂直な速度成分v⊥を獲得し電場ドリフトを伴ったサイクロトロン運動を始める。それと同時に,磁力線に平行な電場成分のため,v//は減速を受ける。v⊥はドリフト速度の2倍まで大きくなりうるが,電場層の厚さが有限なため,最初の層から出る時に持っていたv⊥に応じて,次の新たな電場層のガイディングセンターの周りでサイクロトロン運動する。最終的に電場層を通り抜けた時にはv⊥がv//と同じくらいになり,充分なピッチ角散乱を受けたことがわかる。

図2と同様の追跡をさまざまなエネルギーとピッチ角で入射した電子について行った結果を図3に示す。左より,入射電子,電場層で反射された電子,そして電場層を通過した電子の速度分布である。ウェイク境界の電位差を越えるだけの運動エネルギーを持っていない電子は反射され,それ以上のエネルギーを持つものだけが透過している。透過電子は,電位差分の位置エネルギーに相当する運動エネルギーを失っているだけでなく,磁力線垂直な速度成分を獲得し,入射時に磁力線方向の10度以内だったピッチ角が,60度程度まで広がっていることがわかる(Nakagawa and Iizima,2006)。

図2,図3よりわかるとおり,電場層を通過後の電子のv⊥はドリフト速度uD= E/B (Eは電場,Bは磁場強度)の2倍ないし3倍程度となった。ピッチ角が十分散乱されているならばv⊥〜 v//と考えられ,GEOTAILで観測された波より v//がわかっているので,ドリフト速度uDは0.02c-0.03cと推定される。磁場強度B=6[nT]を代入すれば電場強度Eはおよそ28-40[mV/m]となる。これはLunar Prospector衛星による電場観測結果よりはるかに強い値である。Lunar Prospector衛星からの粒子観測に基づくポテンシャルの調査では,月の真裏付近で300Vの電位降下が報告されているものの(Halekas et al., 2005),40[mV/m]もの強い電場はウェイク境界では報告されていない。同じ電圧降下300Vで電場強度40[mV/m]となるには,厚さ7.5kmという非常に薄い電場層でなければならない。ウェイク境界の電場層は電子とイオンの熱速度の差で形成されるため,月から後方に離れるにつれ厚さが増すと考えれば,この電場層の位置は,太陽風から見て側方のterminatorと呼ばれる領域からわずか18km下流となってしまう。これほど月に近い位置では,ウェイク境界の電場というよりむしろ月面に付着する電子による電場の寄与のほうが大きいとも考えられる。
ピッチ角の広がったビーム入射により,実際に観測されたようなホイッスラー波が励起されるかどうかを,1次元の電磁粒子コード(Birdsall and Langdon, 1985) を用いたシミュレーションによって実験した。背景の等方的な電子(熱速度は光速cの1.4×10-2倍,約50eVに相当)と冷たいイオンに対し,10%のリングビーム電子(v//〜6.2×10-2c,すなわち約1keVに相当, v⊥= 2v//) を磁力線(x方向)に沿って入射し,波の発生を観察した。数値実験に際しては,時間はプラズマ周波数ωpの逆数,距離はそれに光速cを掛けた値で規格化した。計算領域の長さは102.4c/ωp,グリッド数は1024,粒子数は102400個とした。計算領域の長さは,GEOTAILで観測された波(波長λ= 6.6c/ωp)が10波長以上入るように設定したものである。
図4(a) はΩe/ωp= 10-2 の場合の磁場の横波成分(y成分)の変動を,縦軸を距離x,横軸を時間tとして表示したものである。次第に電場の山が波となって進行していくのがわかるが,進行方向はビームと同方向である。しかしながら,磁場に対して密度を小さくしていくと(Ωe/ωpを大きくしていくと)波の進行方向が変わっていくことがわかった。図4(b) はΩe/ωp= 3×10-2の場合であるが,波の進行が止まり,磁場y成分は波というより構造のように見える。 図4(c) は Ωe/ωp= 5×10-2の場合で,磁場構造がビームとは逆方向に進行していく様子が見える。
(a)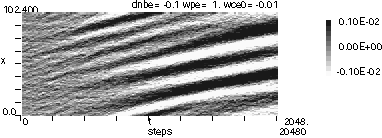
(b)
(c)
しかしながら,図4(c)に現れた波は当初予想したサイクロトロン共鳴で励起されたと考えるには波数,周波数ともに小さすぎることがわかる。図4(c)の磁場変動y成分をそれぞれ,時間,空間の2次元のフーリエ変換をして得たω-k ダイアグラムを図5に示す。曲線はホイッスラー波の分散曲線(但しリングビームを仮定しない場合),右下がりの直線がサイクロトロン共鳴を表す。ホイッスラー波とのサイクロトロン共鳴はこれらの交点に現れると予想されたが,観測された波は波数,周波数とも,これよりずっと小さかった。この理由として,(1) ホイッスラー波の分散曲線を求める際にリングビーム状の電子速度分布を考慮しなかったことがひとつの可能性として考えられるが,(2) 得られた磁場変動が,サイクロトロン共鳴による励起ではなかった,とも考えられる。励起周波数は予想とは異なっていたが,この周波数ω〜0.02Ωeは,実際にGEOTAILで観測されたホイッスラー波の(太陽風に乗った系で見た)周波数2.3×10-2Ωeと近かった。
参考文献
Birdsall , C. K., and A. B. Langdon, Plasma physics via computer simulation, Institute of Physics Publishing, Bristol and Philadelphia, 1985.
Fairfield, D. H., Whistler waves observed upstream from collisionless shocks, J. Geophys. Res., 79, pp.1368-1378, 1974.
Farrell, W. M., R. J. Fitzenreiter, C. J. Owen, J. B. Byrnes, R. P. Lepping, K. W. Ogilvie, F. Neubauer, Upstream ULF waves and energetic electrons associated with the lunar wake: Detection of precursor activity, Geophys. Res. Lett., 23, pp.1271-1274, 1996.
Futaana, Y., S. Machida, T. Saito, A. Matsuoka, and H. Hayakawa, Counterstreaming electrons in the near vicinity of the moon observed by plasma instruments on board NOZOMI, J. Geophys. Res., 106, pp.18729-18740, 2001.
Halekas, J.S,S.D.Bale,D.L.Mitchell,and R. P. Lin, Electrons and magnetic fields in the lunar plasma Wake, J. Geophys. Res., 110, A07222, doi10.1029/2004JA010991, 2005.
Lin, R. P., D. L. Mitchell, D. W. Curtis, K. A. Anderson, C. W. Carlson, J. McFadden, M. H. Acu~na,
L.L. Hood, and A. Binder, Lunar surface magnetic fields and their interaction with the solar wind: Results from Lunar Prospector, Science, 281, pp.1480-1484, 1998.
Lyon, E. F., H. S. Bridge, and J. H. Binsack, Explorer 35 plasma measurements in the vicinity of the moon, J. Geophys. Res., 72, pp.6113-6117, 1967.
Ness, N. F., and K. H. Shatten, Detection of interplanetary magnetic field fluctuations stimulated by the lunar wake, J. Geophys. Res., 74, pp.6425-6438, 1969.
Nakagawa, T., Y. Takahashi, and M. Iizima, GEOTAIL observation of upstream ULF waves associated with lunar wake, Earth Planets Space, 55, pp.569-580, 2003.
Nakagawa, T. and M. Iizima, Pitch angle diffusion of electrons at the boundary of the lunar wake, Earth Planets Space, 57, pp.885-894, 2005.
Nakagawa, T. and M. Iizima, A reexamination of pitch angle diffusion of electrons at the boundary of the lunar wake, Earth Planets Space, 58, (No. 5), pp. e17-e20, 2006.
Ogilvie, K. W., J. T. Steinberg, R. T. Fitzenreiter, C. J. Owen, A. J. Lazarus, W. M. Farrell, and R. B. Torbert, Observation of the lunar plasma wake from the WIND spacecraft on December 27, 1994, Geophys. Res. Lett., 23, pp.1255-1258, 1996.
Owen, C. J., R. P. Lepping, K. W. Ogilvie, J. A. Slavin, W. M. Farrell, and J. B. Byrnes, The lunar wake at 6.8 RL:WIND magnetic field observations, Geophys. Res. Lett., 23, pp.1263-1266, 1996.
関連論文(和文)
2003年9月10-11日 ULF波動で知る月のウェイクのポテンシャル
2005年12月12日 月のウェイク境界におけるホイッスラー波の励起