増加率のグラフ
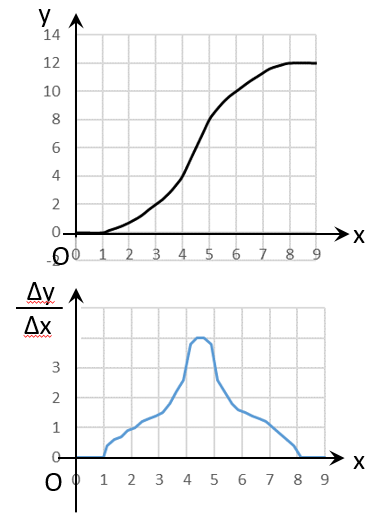
増加率のグラフは2番目の例のような階段状ではないところがポイントです。
y のグラフの違いは、カクカクしてなくて、変化がなめらかなこと。たとえば
x=1 から x=3 までの区間で 同じように増えているわけではなく
(拡大図)
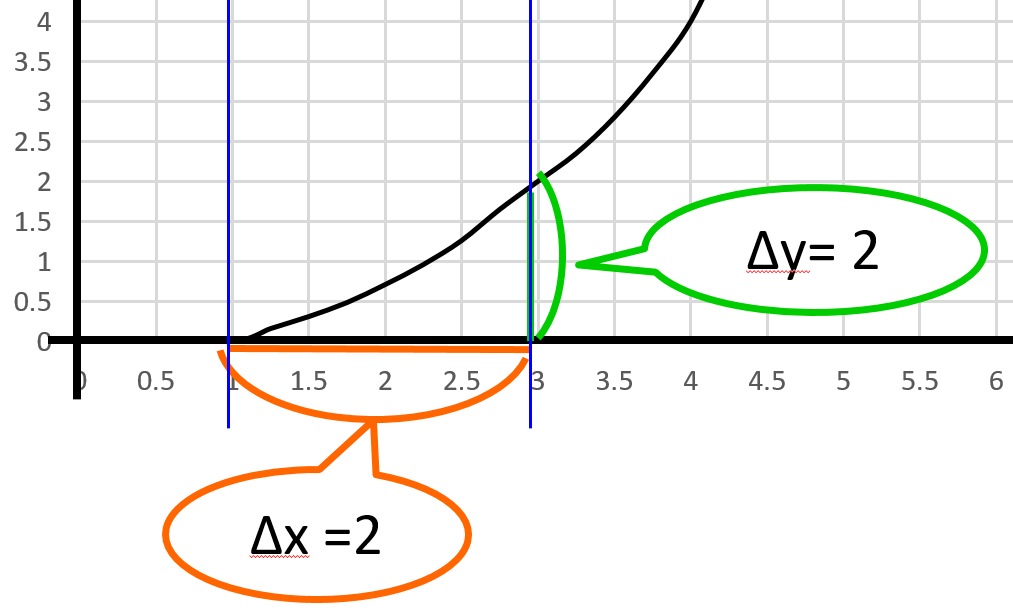
x=1 から x=3 までの区間を前半と後半に分けてみると
前半は少なめ \( \frac{\Delta y}{\Delta z} = 0.7 \)、
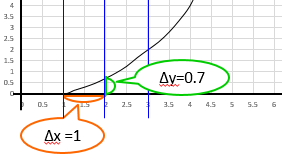
後半は多め \( \frac{\Delta y}{\Delta z} = 1.3 \)
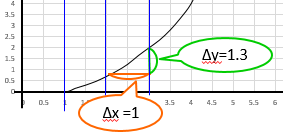
だから、増加率は、x=1 から x=3 までずっと1というわけではなく
前半 少なめ、後半 多めになっています。
\(\Delta x \) は1って決まってるわけではないですよね。
さらに細かく分けてみると
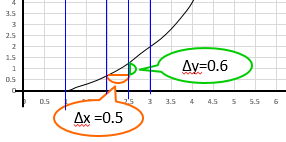
x=2 から x=2.5 までは
\(\Delta x =0.5\)、\(\Delta y =0.6\)なので \( \frac{\Delta y}{\Delta x} = \frac{0.6}{0.5} = 1.2 \)
x=2.5 から x=3 までは
\(\Delta x =0.5\)、\(\Delta y =0.7\)なので \( \frac{\Delta y}{\Delta x} = \frac{0.7}{0.5} = 1.4 \) になるでしょう
だから、増加率は、x=2 から x=3 の間も、ずっと1.3 というわけではなく
前半 少なめ、後半 多めになっています。
もっと詳しく、\(\Delta x =0.2\) とかにしてみると
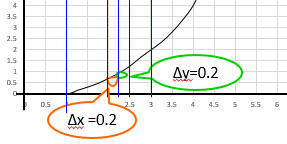
\(\Delta x =0.2\)、\(\Delta y =0.2\)なので \( \frac{\Delta y}{\Delta x} = \frac{0.2}{0.2} = 1.0 \)
さらに細かく分けて
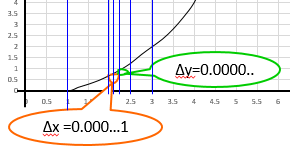
\(\Delta x \) をどんどん細かくして棒グラフを細く細くしていくと
増加率\( \frac{\Delta y}{\Delta x} \) のグラフの解像度がどんどん上がって
ギザギザじゃなく、いつかなめらかなグラフになりそうですね。
\(\Delta x \) は極限まで詳しくした方が正確になる気がしますね。
次のページ