-
- 実習こたえあわせ
-
5つ目は例えば
\begin{align}
\sin{\theta }= \frac{高さ}{斜辺} = \frac{1.56\ cm}{2.0\ cm}=0.78
\end{align}
多少の誤差はあっても構いません。
\(\sin{\theta }=\) 0.75 ~0.8 くらいになっていたらOKです。
6つ目以降は、
補助線を入れて測ると
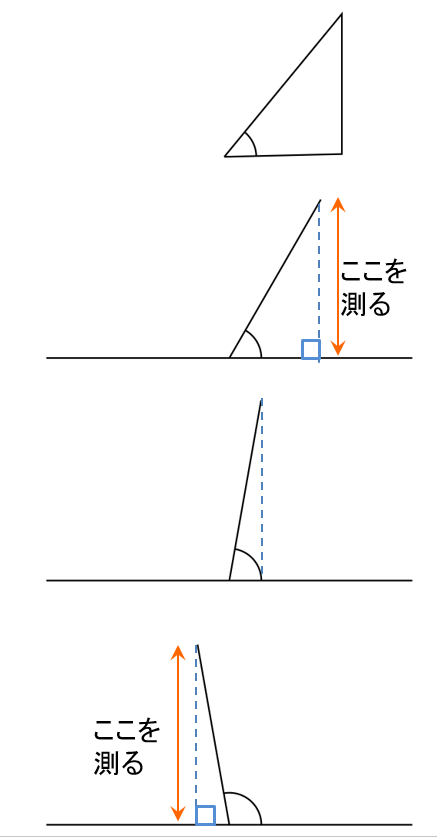
同様に、
6つめ \(\sin{\theta }=\) 0.85 ~0.87 くらい
7つめ \(\sin{\theta }=\) 0.98 ~0.99 くらい
8つめ \(\sin{\theta }=\) 0.85 ~0.87 くらい
-
正三角形
から30°60°の三角比
-
正三角形は3辺の長さが等しく、3つの角も等しいです。
三角形の内角の和は180°なので、一つの角度は60°ですよね。
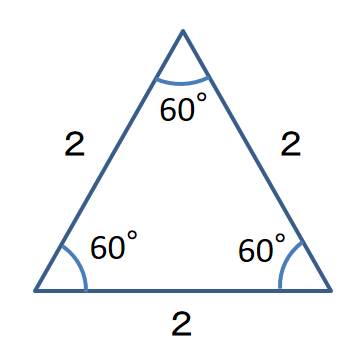
正三角形は2等辺三角形でもあるので、
頂点から向いの辺に下した垂線は、辺を2等分しますね。
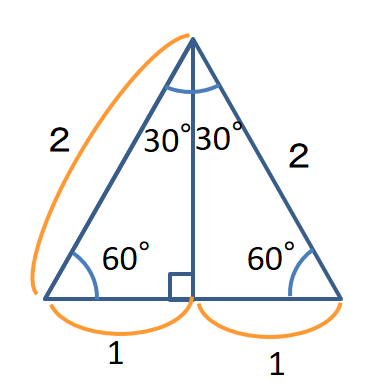
半分だけ見ると直角三角形です。
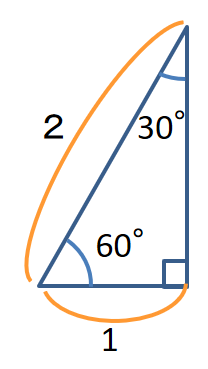
これをみただけでも
$\cos{ 60°} = \frac{1}{2}$ ということがわかります。
では
$\sin{ 60°} $ は?これを知るには「高さ」が必要です。
高さを求めるのに使うのがこれ
底辺2+高さ2=斜辺2
-
(ピタゴラスの定理) 証明してください
|



