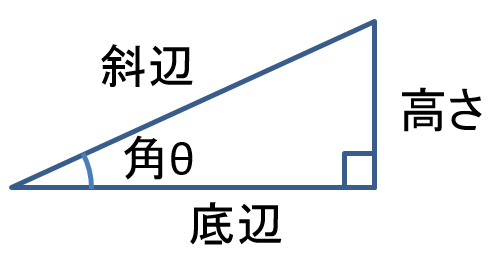
底辺2+高さ2=斜辺2
-
(ピタゴラスの定理)
証明
4つ集めて四角にして
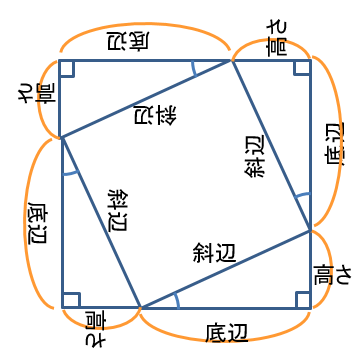
一辺の長さが「底辺+高さ」なので
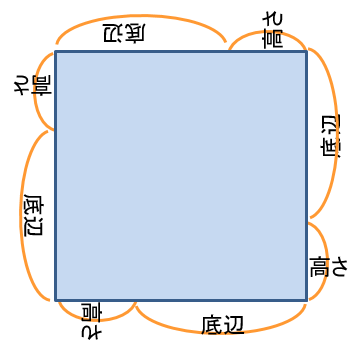
外側の正方形の面積は(底辺+高さ)2
ここから三角形の面積を4つ分引くと引くと
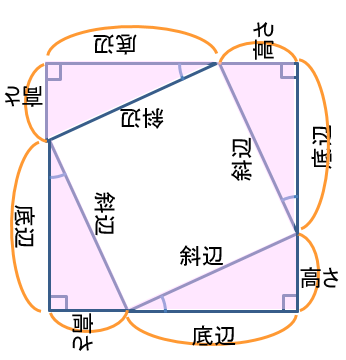
内側の正方形の面積 斜辺2になるはず
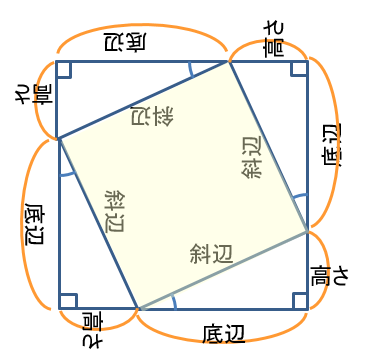
(底辺+高さ)2 - 4(底辺)(高さ)/2 = 斜辺2
展開すると
底辺2+2(底辺)(高さ)+高さ2- 2(底辺)(高さ)= 斜辺2
よって
底辺2+高さ2 = 斜辺2
- 使用例
-
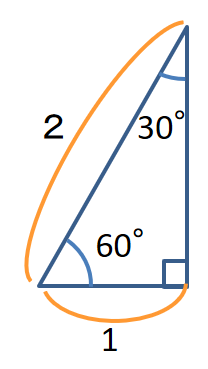
底辺2+高さ2 = 斜辺2 底辺が1、斜辺が2なら
12 +高さ2 = 22
1 +高さ2 = 4 なので
高さ2 = 3
つまり
高さ = $\sqrt{3}$
$\sin{ 60°} =\frac{\sqrt{3}}{2}$
$\tan{ 60°} =\frac{\sqrt{3}}{1}$
30°が左下に来るように置けば
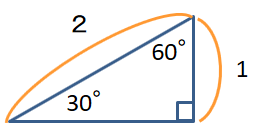
$\sin{ 30°} =\frac{1}{2}$
$\cos{ 30°} =\frac{\sqrt{3}}{2}$
$\tan{ 30°} =\frac{1}{\sqrt{3}}$
次のページ