- 正方形から45°の 三角比
-
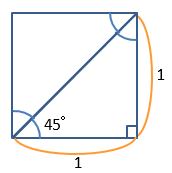
正方形を対角線で二つに分けると直角三角形
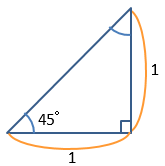
図を見ただけで
$\tan{ 45°} =\frac{1}{1} = 1$ が分かりますが
サイン、コサインを求めるには「斜辺」が必要です。
底辺2+高さ2 = 斜辺2 底辺が1、高さも1なら
12+ 12 = 斜辺2
2 = 斜辺2
つまり
斜辺 = $\sqrt{2}$
よって
$\sin{ 45°} =\frac{1}{\sqrt{2}}$
$\cos{ 45°} =\frac{1}{\sqrt{2}}$
次のページ