-
三角比から底面、高さを求める
-
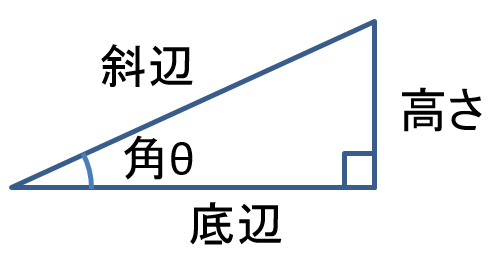
ここまでは、斜辺、底辺、高さから
サインやコサインの値を求めてきましたが、
\begin{align}
\sin{\theta }= \frac{高さ}{斜辺} , \quad
\cos{\theta }= \frac{底辺}{斜辺} , \quad
\end{align}
サインの式やコサインの式の両辺に「斜辺」をかければ
\begin{align}
{斜辺}\sin{\theta }= {高さ}, \quad
{斜辺} \cos{\theta }= {底辺}
\end{align}
と変形できるので、斜辺とサインやコサインの値がわかれば、逆に
未知の「高さ」や「底辺の長さ」を知ることもできます。
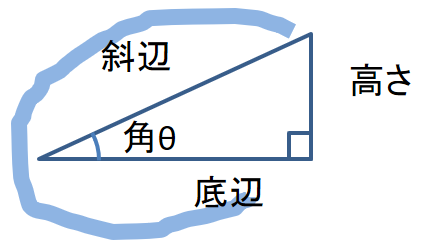
- 例題:下図で斜辺の長さが $r$ のとき、底辺と高さを求めよ
-

底辺がでてくるのはcosの式
\begin{align}
\cos{\theta }= \frac{底辺}{ r } \quad \quad
\end{align}
両辺に $r$ をかけて
\begin{align}
r \cos{\theta }= {底辺}
\end{align}
左右入れ替えて 底辺$= r \cos{\theta }$
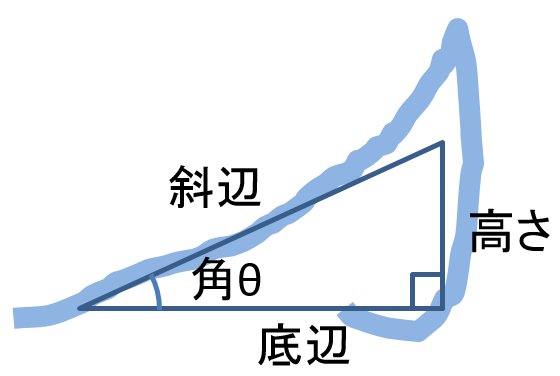
高さがでてくるのはsinの式
\begin{align}
\sin{\theta }= \frac{高さ}{ r } \quad \quad
\end{align}
両辺に $r$ をかけて
\begin{align}
r \sin{\theta }= {高さ}
\end{align}
左右入れ替えて 高さ$= r \sin{\theta }$
かんたんだね!
次のページ
|



