-
ベクトル
$ \left( \begin{array}{c} 4 \\ 2 \end{array} \right) $
を図示すると、
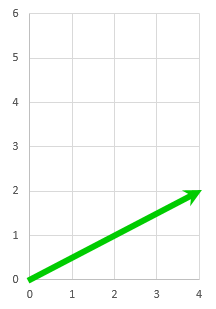 横に 4, 縦に 2
のこういう図 横に 4, 縦に 2
のこういう図
ではこれは?
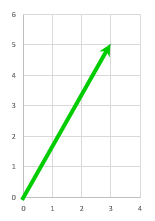 横に 3, 縦に 5なので
横に 3, 縦に 5なので
ベクトル
$ \left( \begin{array}{c} 3 \\ 5 \end{array} \right) $
ですよね
ベクトル
$ \left( \begin{array}{c} 3 \\ 0 \end{array} \right) $
を図示すると
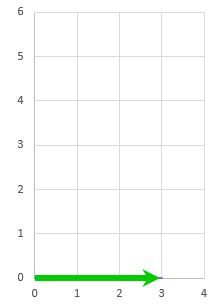 横に 3, 縦に 0 のこんな矢印 横に 3, 縦に 0 のこんな矢印
このベクトルを、角度 $\theta$ 回転すると
(角度は
$x$ 軸から第一象限に向かう方向に測ります。)
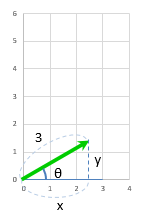 \begin{align}
\cos{\theta }= \frac{x}{ 3} より、横 x= 3\cos{\theta}\quad \\
\sin{\theta }= \frac{y}{ 3} より、縦 y= 3\sin{\theta}\quad
\end{align}
なので回転後のベクトルは
$ \left( \begin{array}{c}3\cos{\theta} \\ 3\sin{\theta} \end{array} \right) $
ですね。
\begin{align}
\cos{\theta }= \frac{x}{ 3} より、横 x= 3\cos{\theta}\quad \\
\sin{\theta }= \frac{y}{ 3} より、縦 y= 3\sin{\theta}\quad
\end{align}
なので回転後のベクトルは
$ \left( \begin{array}{c}3\cos{\theta} \\ 3\sin{\theta} \end{array} \right) $
ですね。
ベクトル
$ \left( \begin{array}{c} 0 \\ 5 \end{array} \right) $
を図示すると、
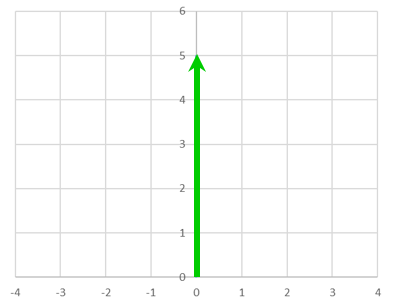 横に 0, 縦に 5 のこういう図
横に 0, 縦に 5 のこういう図
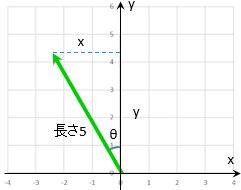
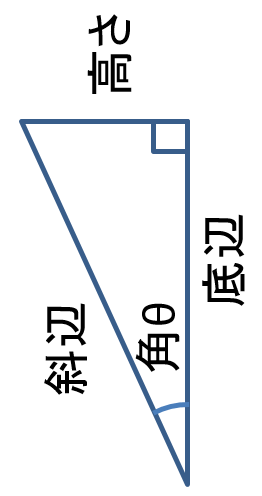
このベクトルを、角度 $\theta$ 回転すると
\begin{align}
\sin{\theta }&= \frac{|x|}{ 5} より、&横 |x|= 5\sin{\theta}\quad \\
\cos{\theta }&= \frac{y}{ 5} より、&縦 y= 5\cos{\theta}\quad
\end{align}
$x$ 軸の矢印は、右に行くと $x$ が増えることを表しています。
回転によって $x$ は原点より左、マイナス側に行ってしまったので
横 $x= - 5\cos{\theta}$
なので回転後のベクトルは
$ \left( \begin{array}{r} -5\sin{\theta} \\ 5\cos{\theta} \end{array} \right) $
ですね。
では。
ベクトル
$ \left( \begin{array}{c} 3 \\ 5 \end{array} \right) $
を、

角度 $\theta$ 回転したらどんなベクトルになるか求めてください。
困ったらここ
|
 横に 4, 縦に 2
のこういう図
横に 4, 縦に 2
のこういう図 横に 3, 縦に 5なので
横に 3, 縦に 5なので 横に 3, 縦に 0 のこんな矢印
横に 3, 縦に 0 のこんな矢印 \begin{align}
\cos{\theta }= \frac{x}{ 3} より、横 x= 3\cos{\theta}\quad \\
\sin{\theta }= \frac{y}{ 3} より、縦 y= 3\sin{\theta}\quad
\end{align}
なので回転後のベクトルは
$ \left( \begin{array}{c}3\cos{\theta} \\ 3\sin{\theta} \end{array} \right) $
ですね。
\begin{align}
\cos{\theta }= \frac{x}{ 3} より、横 x= 3\cos{\theta}\quad \\
\sin{\theta }= \frac{y}{ 3} より、縦 y= 3\sin{\theta}\quad
\end{align}
なので回転後のベクトルは
$ \left( \begin{array}{c}3\cos{\theta} \\ 3\sin{\theta} \end{array} \right) $
ですね。
 横に 0, 縦に 5 のこういう図
横に 0, 縦に 5 のこういう図

