-
ベクトル
$ \left( \begin{array}{c} 3 \\ 5 \end{array} \right) $
を、角度 $\theta$ 回転したらどんなベクトルになるか
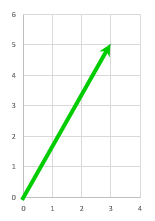
いきなりやろうとして悩む1年生が多いですが、
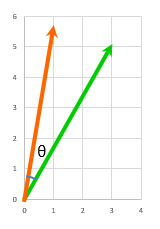
いきなりやろうとしないで
$ \left( \begin{array}{c} 3 \\ 5 \end{array} \right)
=
\left( \begin{array}{c} 3 \\ 0 \end{array} \right)
+
\left( \begin{array}{c} 0 \\ 5 \end{array} \right)
$
と2つのベクトルの和と考えて、
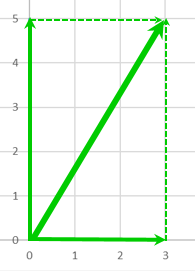
それぞれ回転してから
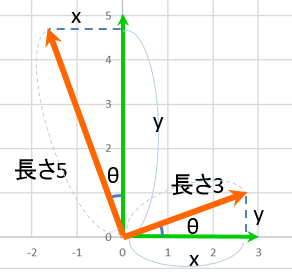
足せば簡単です。
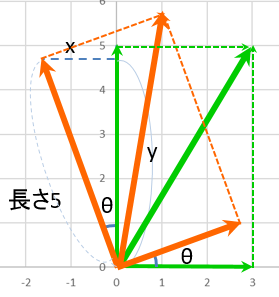
「それぞれ回転する」ところは、前のページでもみたように

ベクトル
$ \left( \begin{array}{c} 3 \\ 0 \end{array} \right) $を角度 $\theta$ 回転したベクトルは $ \left( \begin{array}{c}3\cos{\theta} \\ 3\sin{\theta} \end{array} \right) $ 、
ベクトル
$ \left( \begin{array}{c} 0 \\ 5 \end{array} \right) $を角度 $\theta$ 回転したベクトルは $ \left( \begin{array}{r} -5\sin{\theta} \\ 5\cos{\theta} \end{array} \right) $ なので
回転してから足すと
$ \left( \begin{array}{c}3\cos{\theta} \\ 3\sin{\theta} \end{array} \right)
+
\left( \begin{array}{r} -5\sin{\theta} \\ 5\cos{\theta} \end{array} \right)
=
\left( \begin{array}{r} 3\cos{\theta}-5\sin{\theta} \\ 3\sin{\theta}+5\cos{\theta}
\end{array} \right) $

よって、
ベクトル
$ \left( \begin{array}{c} 3 \\ 5 \end{array} \right) $を角度$\theta$回転させてできるベクトルの座標は
$ \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)
=
\left( \begin{array}{r} 3\cos{\theta}-5\sin{\theta} \\ 3\sin{\theta}+5\cos{\theta}
\end{array} \right) $
この式は、行列を使って
$ \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)
=
\left( \begin{array}{rr}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta}& \cos{\theta}
\end{array} \right)
\left( \begin{array}{r}
3\\
5
\end{array} \right) $
と書くことができます(線形代数)。
もとのベクトルが
$ \left( \begin{array}{c} 3 \\ 5 \end{array} \right) $じゃなかったとしても
同じような計算ができるね。
もとのベクトルが
$ \left( \begin{array}{c} 4 \\ 7 \end{array} \right) $だったら
$ \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)
=
\left( \begin{array}{rr}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta}& \cos{\theta}
\end{array} \right)
\left( \begin{array}{r}
4\\
7
\end{array} \right) $ になるし
もとのベクトルが
$ \left( \begin{array}{c} x_0 \\ y_0 \end{array} \right) $だったら
$ \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)
=
\left( \begin{array}{rr}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta}& \cos{\theta}
\end{array} \right)
\left( \begin{array}{r}
x_0\\
y_0
\end{array} \right) $
でいいよね。
次へ
|






