-
ベクトル
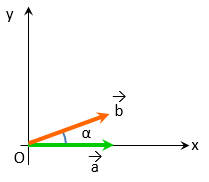
$\vec{a} = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) $
を角度 $\alpha$(アルファ) 回転したベクトル
$\vec{b}$ の座標は
$ \left(
\begin{array}{c} x_b \\ y_b \end{array}
\right)
=
\left(
\begin{array}{rr}
\cos{\alpha} & -\sin{\alpha} \\
\sin{\alpha} & \cos{\alpha}
\end{array}
\right)
\left(
\begin{array}{r}
1\\
0
\end{array}
\right)
=
\left(
\begin{array}{r}
\cos{\alpha} \\
\sin{\alpha}
\end{array}
\right)
$
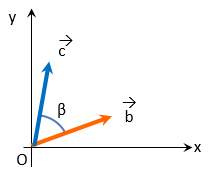
このベクトル
$\vec{b} $
をさらに角度 $\beta$(ベータ) 回転したベクトル
$\vec{c}$ の座標は
$ \left(
\begin{array}{c} x_c \\ y_c \end{array}
\right)
=
\left(
\begin{array}{rr}
\cos{\beta} & -\sin{\beta} \\
\sin{\beta} & \cos{\beta}
\end{array}
\right)
\left(
\begin{array}{r}
\cos{\alpha} \\
\sin{\alpha}
\end{array}
\right)
$
注:回転を表す行列は、2行2列の行列です。
$\cos{\beta}$ と $-\sin{\beta}$の間がくっつかないよう、離して書く
行列とベクトルの掛け算を実行すると
$ \left(
\begin{array}{c} x_c \\ y_c \end{array}
\right)
=
\left(
\begin{array}{c}
\cos{\beta}\cos{\alpha}-\sin{\beta}\sin{\alpha} \\
\sin{\beta}\cos{\alpha}+\cos{\beta}\sin{\alpha}
\end{array}
\right)
$
注:掛け算したので右辺はベクトルです。
$\cos{\beta}\cos{\alpha}-\sin{\beta}\sin{\alpha}$ で1つの数字なので、間を離さずくっつけて書く
足し算や掛け算は順序が反対でも同じなので
$ \left(
\begin{array}{c} x_c \\ y_c \end{array}
\right)
=
\left(
\begin{array}{c}
\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}
\\
\sin{\alpha}\cos{\beta}+
\cos{\alpha}\sin{\beta}
\end{array}
\right)
$ でもいいです。
ところで、角度α回転してさらに角度β回転するのと、
角度(α+β)一気に回転するのと、結果は同じですよね。
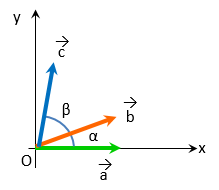
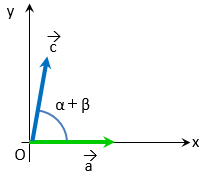
ベクトル
$\vec{a} = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) $
を角度 $(\alpha + \beta )$ 回転したベクトル
$\vec{c}$ の座標は
$ \left(
\begin{array}{c} x_c \\ y_c \end{array}
\right)
=
\left(
\begin{array}{rr}
\cos{(\alpha + \beta )} & -\sin{(\alpha + \beta )} \\
\sin{(\alpha + \beta )} & \cos{(\alpha + \beta )}
\end{array}
\right)
\left(
\begin{array}{r}
1\\
0
\end{array}
\right)
=
\left(
\begin{array}{r}
\cos{(\alpha + \beta )} \\
\sin{(\alpha + \beta )}
\end{array}
\right)
$
一気に求めたベクトル
$\vec{c} $ と、小分けに求めたベクトル
$\vec{c} $ は同じなので
$
\left(
\begin{array}{r}
\cos{(\alpha + \beta )} \\
\sin{(\alpha + \beta )}
\end{array}
\right)
=
\left(
\begin{array}{c}
\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}
\\
\sin{\alpha}\cos{\beta}+
\cos{\alpha}\sin{\beta}
\end{array}
\right)
$
となります。つまり
\begin{align}
\cos{(\alpha + \beta )} =
\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta} \\
\sin{(\alpha + \beta )} = \sin{\alpha}\cos{\beta}+
\cos{\alpha}\sin{\beta}
\end{align}
いうことがわかります。これを加法定理といいます(教科書p16)。
とても便利で様々なところに使われます。
使用例へ
|



