- 加法定理の使用例 1
-
電卓なしでふつう覚えているのは30°、45°、 60°ですが
たとえば 75°なら、 30°+45°
と考えることによって、加法定理を使って
\begin{align}
\cos{(30° + 45° )} =
\cos{30°}\cos{45°}-\sin{30°}\sin{45°} \\
\sin{(30° + 45° )} = \sin{30°}\cos{45°}+
\cos{30°}\sin{45°}
\end{align}
と書けるので、これに値を代入すれば
\begin{align}
\cos{(30° + 45° )}
=
\frac{\sqrt{3}}{2} \frac{1}{\sqrt{2}}
-
\frac{ 1 }{2} \frac{1}{\sqrt{2}} \\
\sin{(30° + 45° )}
=
\frac{ 1 }{2} \frac{1}{\sqrt{2}}
+
\frac{\sqrt{3}}{2} \frac{1}{\sqrt{2}}
\end{align}
のように値を求めることができます。
90°を、 30°+60°と考えると
\begin{align}
\sin{(30° + 60° )} = \sin{30°}\cos{60°}+
\cos{30°}\sin{60°}
\end{align}
と書けるので、これに値を代入すれば
\begin{align}
\sin{(30° + 60° )}
=
\frac{1}{2}
\frac{1}{2}
+
\frac{\sqrt{3}}{2}
\frac{\sqrt{3}}{2}
=
\frac{1}{4}+
\frac{3}{4}
= 1
\end{align}
$\sin{(89.99999 ...° )} $から考えたときと
同じになりました。
- 加法定理の使用例 2
-
\begin{align}
\cos{(\alpha + \beta )} =
\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}
\end{align}
の $\beta$ のところに $-\beta$ を代入すれば、
\begin{align}
\cos{(\alpha - \beta )} =
\cos{\alpha}\cos{(-\beta)}-\sin{\alpha}\sin{(-\beta)}
\end{align}
になりますが、角度がマイナスになった時、
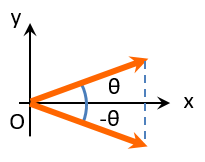
コサインは値が変わらず $\cos{(-\beta)}=\cos{\beta}$
サインは符号が反転する $\sin{(-\beta)} =-\sin{\beta} $ ので
\begin{align}
\cos{(\alpha - \beta )} =
\cos{\alpha}\cos{\beta}-\sin{\alpha}(-\sin{\beta} )
\end{align}
つまり
\begin{align}
\cos{(\alpha - \beta )} =
\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}
\end{align}
最初の式に並べると
\begin{align}
\cos{(\alpha + \beta )} =
\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta} \\
\cos{(\alpha - \beta )} =
\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}
\end{align}
右辺は、半分同じで、半分符号違いですから、
この2本を足すと$\sin{\alpha}\sin{\beta}$が消えて$
\cos{\alpha}\cos{\beta}$が残り、
この2本を引くと$
\cos{\alpha}\cos{\beta}$が消えて$\sin{\alpha}\sin{\beta}$が残り、
\begin{align}
\cos{(\alpha + \beta )} + \cos{(\alpha - \beta )} = 2
\cos{\alpha}\cos{\beta}\\
\cos{(\alpha + \beta )} - \cos{(\alpha - \beta )} = 2\sin{\alpha}\sin{\beta}
\end{align}
両辺を2で割り左右入れ替えると
\begin{align}
\cos{\alpha}\cos{\beta}=
\frac{\cos{(\alpha + \beta )} + \cos{(\alpha - \beta )} }{2}
\\
\sin{\alpha}\sin{\beta}=
\frac{
\cos{(\alpha + \beta )} - \cos{(\alpha - \beta )} }{2}
\end{align}
この式のすごいところは、サインやコサインの掛け算を、
コサインの足し算や引き算に直せるところです。
同じように
\begin{align}
\sin{(\alpha + \beta )} = \sin{\alpha}\cos{\beta}+
\cos{\alpha}\sin{\beta}
\\
\sin{(\alpha - \beta )} = \sin{\alpha}\cos{\beta}-
\cos{\alpha}\sin{\beta}
\end{align}
から、
\begin{align}
\sin{(\alpha + \beta )} +\sin{(\alpha - \beta )}= 2\sin{\alpha}\cos{\beta}
\end{align}
2で割って
\begin{align}
\sin{\alpha}\cos{\beta}=
\frac{
\sin{(\alpha + \beta )} +\sin{(\alpha - \beta )}}{2}
\end{align}
サインとコサインの掛け算は、サインの足し算で書き直せるのです。
この性質はとても便利で、通信にも情報処理にも使います。
今後の専門科目の勉強に繰り返し出てくることになります。
次へ
|
