-
\( f(x) = \sin{x}\) の 導関数を求めようとしてでてきた
\begin{align} \lim_{h \rightarrow 0}
\frac{\sin{({h\over 2})} }
{({h \over2}) }
\end{align}
角度 $({h\over 2})$ を $\theta$ とかくと
\begin{align} \lim_{\theta \rightarrow 0}
\frac{\sin{\theta} }
{\theta }
\end{align}
ですね。「サイン角度」と「角度」の比は、
角度が0に近づくとどうなるのでしょうか。
ここから、この値を求めていきます。
やりかけの
\( f(x) = \sin{x}\) の 導関数の問題は
(余白5行くらい残して)いったん置いて、
新しいページの最初からノートを書いてください。
-
$\theta \rightarrow 0$ のときの
$
\frac{\sin{\theta} }
{\theta }
$
-
角度 $\theta$ の出てくる話なので、半径1の円に角度 $\theta$ を書いてください。
この図に書き込みをしていくので、大きめに書いてね
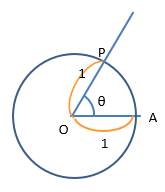
円の中心をO(Origin=原点のOオーです)とし、
$\angle$AOP が角度 $\theta$ になるように、円周上に点A と点P をとります。
- 扇形AOP の面積
-
扇形AOP の面積 S1 は、角度に比例しますよね。
角度が $2\pi $なら円なので、円の面積 $\pi \cdot 1\cdot 1$
角度が $\theta$ なら S1
てことは
扇形の面積 S1:円の面積 $\pi $ = 角度$\theta$ : 1周$2\pi $
\begin{align}
\frac{扇形の面積 S_1}{円の面積\pi}
=
\frac{\theta}{2\pi}
\end{align}
両辺に$\pi$かければ、
扇形の面積 S1=$\displaystyle {\theta \over 2}$
- 三角形AOP の面積
-
次に点Aと点Pを線でつないで、三角形AOP の面積S2 を求めてください。
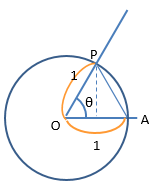
底辺は1ですね。
高さyは、図の点線のところですが、
斜辺が1なので
\begin{align}
\sin{\theta }= \frac{高さy}{斜辺1}
\end{align}
より、
高さ$y= \sin{\theta }$ですね。
よって
三角形AOP の面積S2 =
$\displaystyle {1\over 2}\cdot 1\cdot \sin{\theta} = {\sin{\theta} \over 2}$
- 三角形AOT の面積
-
次に点Aから、線分OAに垂直に線を引いて、
線分OPの延長線と交わった点をTとしてください。
$\angle$OAT には、直角を表す小さな四角□を書いてください。
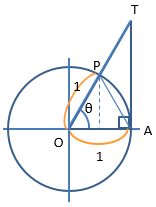
三角形OAT の面積S3 を求めてください。
底辺は1ですね。
高さは線分ATの長さです。角度$\theta $ を使ってかくと
\begin{align}
\tan{\theta }= \frac{線分ATの長さ}{底辺1}
\end{align}
なので線分ATの長さは$\tan{\theta}$ですね。
よって
三角形AOP の面積S3 =
$\displaystyle {1\over 2}\cdot 1\cdot \tan{\theta} = {\tan{\theta} \over 2}$
- はさみうち
-
扇形と三角形の面積を比べると、
三角形AOP の面積S2 < 扇形AOP の面積 S1 < 三角形OAT の面積S3
なので
\begin{align}
{\sin{\theta} \over 2}
<
{\theta \over 2}
<
{\tan{\theta} \over 2}
\end{align}
各項に2をかけても同じなので
\begin{align}
\sin{\theta}
<
\theta
<
\tan{\theta}
\end{align}
1本の式に不等式が2つあるときは、無理に一度に扱わずに
\begin{align}
\sin{\theta}
<
\theta
\quad と\quad
\theta
<
\tan{\theta} \quad の
\end{align}
2つの不等式に分けて考えると考えやすいです。
$\theta $ がプラスなら、
左側の式 $\sin{\theta} < \theta$ の両辺を$\theta $で割って
\begin{align}
{\sin{\theta} \over \theta} < 1
\end{align}
になります。知りたかった$ {\sin{\theta} \over \theta}$ が出てきましたね。
右側の式の $\tan{\theta}$ を書き直すと
\begin{align}
{\theta }
<
{\sin{\theta} \over \cos{\theta}}
\end{align}
$\theta \rightarrow 0$ では、$\cos{\theta}$ は$\cos{ 0 } = 1$ に近いのでプラス、
プラスの数をかけても不等式の大小関係は変わらないので
\begin{align}
{\theta } \cos{\theta}
<
\sin{\theta}
\end{align}
両辺を$\theta $で割ると
\begin{align}
\cos{\theta}
<
{\sin{\theta} \over \theta}
\end{align}
知りたかった$ {\sin{\theta} \over \theta}$ がまた出てきました。
$ {\sin{\theta} \over \theta}$ が出てくる式2本を、
$ {\sin{\theta} \over \theta}$ を中心にまとめると、
\begin{align}
\cos{\theta}
<
{\sin{\theta} \over \theta}
<
1
\end{align}
$\cos{\theta} $ と 1 で挟んであります。
この状態で
$ \theta \rightarrow 0 $します。
両側の極限はどちらも1
\begin{align}
\lim_{\theta \rightarrow 0} \cos{\theta} = \cos{0} = 1 \quad \quad
\lim_{\theta \rightarrow 0}1 = 1
\end{align}
挟んでいる両側がそれぞれ1に収束するので、
挟まれている真ん中の式も1に収束するしかないですよね。
\begin{align}
\lim_{\theta \rightarrow 0}{\sin{\theta} \over \theta} = 1
\end{align}
注意:
\begin{align}
1
<
{\sin{\theta} \over \theta}
<
1 とかかないこと
\end{align}
1より大きく(1ではない)
1より小さい(1ではない)値はないので、
こう書いてしまうと答えがなくなる、、、
もし$\theta$ がマイナスだったら、
プラスの数 $t$ を使って
$\theta =-t$ とかいて代入すると
\begin{align}
\lim_{\theta \rightarrow -0}{\sin{\theta} \over \theta}
=
\lim_{t \rightarrow +0}{\sin{( -t )} \over -t }
\end{align}
と書き換えられますよね。$\sin{( -t )}$ は$-\sin{t}$ なので、
結局同じ計算になりますよね。(教科書p.17)
f(x)=sin(x) の導関数に戻る
|


