-
\( f(x) = \sin{x}\) の 導関数
-
さっき途中まで計算して
\begin{align}f'(x)
&=& \lim_{h \rightarrow 0} \frac
{\quad \cos{(x+{h\over 2})}\sin{({h\over 2})} }
{({h \over2}) }
\end{align}
ここまできてました。
$h \rightarrow 0$ のときはもちろん
${h\over 2}$ も $ \rightarrow 0$ なので
\begin{align}
\lim_{({h\over 2}) \rightarrow 0}
\frac
{\sin{({h\over 2})} }
{({h \over2}) }
= 1
\end{align}
が使えます。よって
\begin{align}f'(x)
&= &\cos{(x+0)} \cdot 1\\
&= &\cos{(x)} \quad \quad \quad
\end{align}
まとめると
\begin{align}
(\sin{ x })' = \cos{(x)}
\end{align}
サインを微分するとコサインになるね。
実はやったことあるよね。
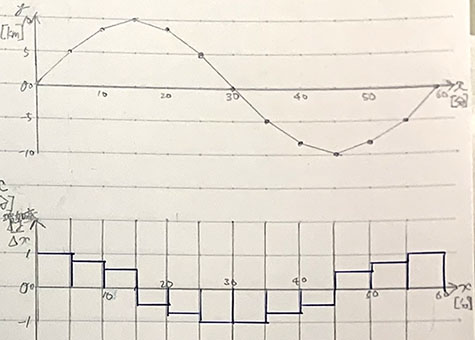
増加率のグラフの形、これはコサインだね!
しみじみ見てみましょう
出だし、yが増加しているので、増加率y' はプラス
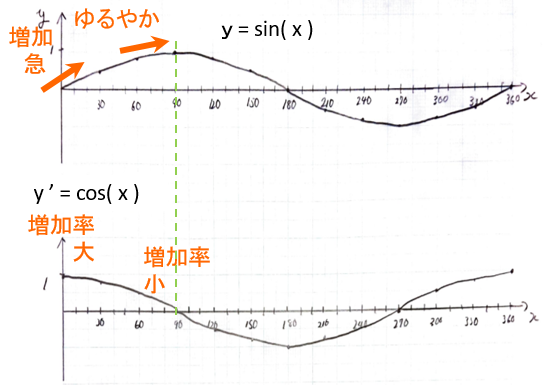
ゆるやかになってくると、小さいプラス
yが減少し始めると、
増加率はマイナス
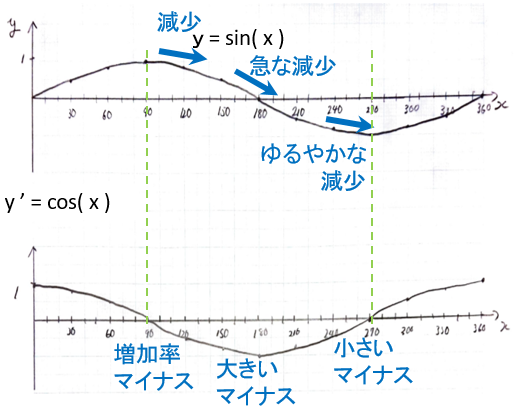
激しい減少だと、大きいマイナス
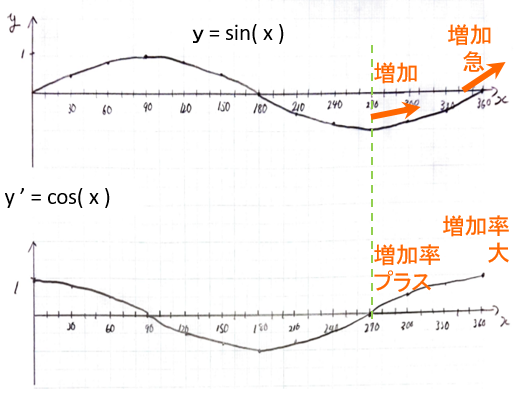
どん底から増え始めると、
yの値はマイナスでも、増加率はプラス
- 次は$f(x)=\cos{(x)}$ の導関数も求めてみよう
-
できたら答え合わせ
|



