解析 I （1回目）関数の増加率

グラフで見た関数 \( f(x)\)

横軸を x 軸、 縦軸を y 軸として、 それぞれの x に対する y の点を打っていけば グラフが書けます。

たとえばこれ

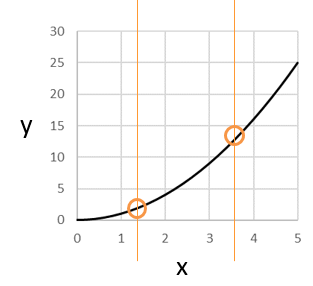
１つの x に対して y の値はただ1つだけなので 「関数」と言えます。

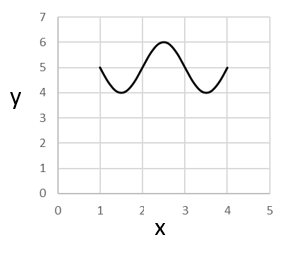
これはどうでしょう？

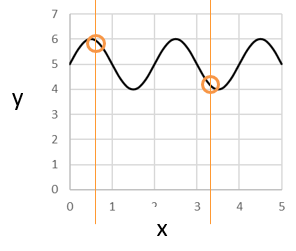
yの値が 6 になるところが何度もでてきますが、それでも、
１つの x に対して y の値はただ1つだけなので 「関数」と言えます。

これはどうでしょう？

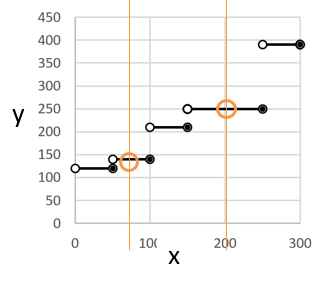
グラフがつながっていませんが、それでも、
１つの x に対して y の値はただ1つだけなので 「関数」と言えます。

これはどうでしょう？

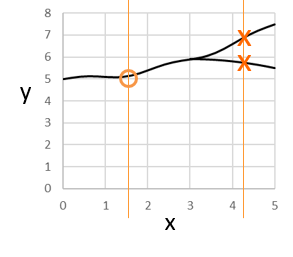
１つの x に対して y の値が2つあるところがありますね。
yがただ1つに決まらないので関数でないということになります。

ではこれは？


関数である　　　　　　　　　　　　 関数でない