解析 I （1回目）関数の増加率

簡単な関数の例

時間 0 分に 0 [km] からバイクで出発して
時間 10 分には 5 [km] の距離まで行けるなら
時間 20 分には 10 [km]
時間 30 分には 15 [km]
時間 40 分には 20 [km] の距離まで行けますよね

グラフにかくとこんなかんじ


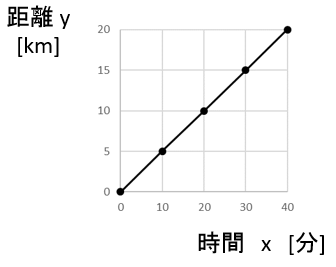
0分から10分までの10分間に 0 [km] から 5 [km] まで進むので

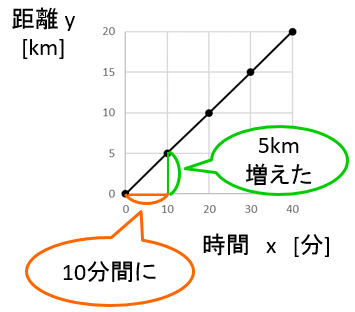
1分あたりにすると 0.5 [km/分] になりますね。
\begin{align}速度 v = \frac{5 [km]}{ 10 [分]}　= 0.5 [km/分]\end{align} 速度 velocity の頭文字をとって $v$ とかきました。


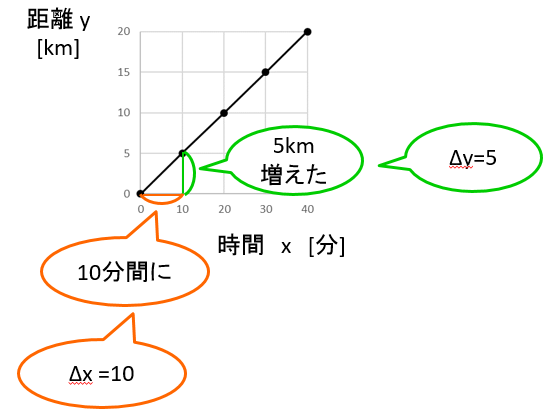
この10 [分]というのは、
x = 0分 から x = 10分 までの、 x の増えた分です。
x の増分を\(\Delta x\)と書き、 デルタx と読みます。

5 [km]のほうは、
y = 0 km から y = 5 kmまでの y の増分 \(\Delta y\)
デルタy と読みます。

速度というのは 距離$y$ の増分 \(\Delta y\)　を
かかった時間　つまりx の増分\(\Delta x\)で割ったものですね \begin{align}速度 v = \frac{\Delta y}{\Delta x}　\end{align} この右辺を y の増加率といいます。

このグラフの別の時間、 x = 20分 から x = 30分 までをとってみると、

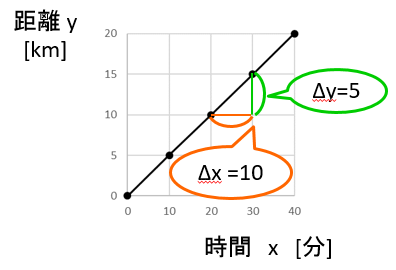
\(\Delta x \) = 30分 - 20分 = 10分
\(\Delta y \) = 15km - 10km = 5km
なので、増加率はやはり
\begin{align}増加率 \frac{\Delta y}{\Delta x}　 = \frac{5 [km]}{10 [分]}　= 0.5 [km/分]\end{align}

さっきと同じ速度でした


次のページ