解析 I （1回目）関数の増加率

ノートにグラフを書く

ここから作業です。ノートを書いていきます。

ノートにグラフを書くときは、ノートの罫線を利用してください。
定規の1cm, 2cm に合わせるとノートの罫線からずれるので、
定規は直線を引くだけに使い、定規の目盛は使わないでください。


ノートの上端と下端には、よく見ると目盛がついているものが多く、
定規や下敷きでこれをつなぐと、方眼紙のように使うことができます。

元のグラフを書く

まず元のグラフを書きます。 グラフに必ず必要なものは
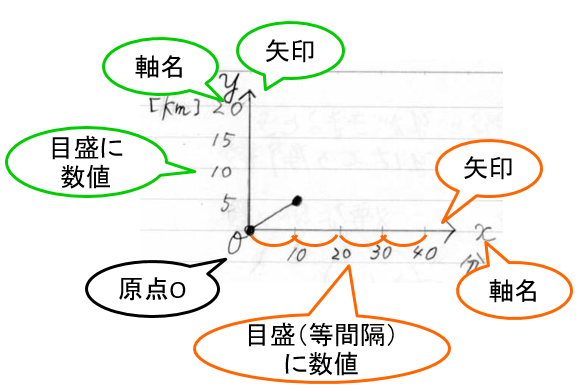
・横軸と、右に行くとx が増えることを示す矢印
・矢印のそばに 軸名 x の文字
・横軸上に、目盛3つ以上と数値（と単位）
・縦軸と、上に行くと yが増えることを示す矢印
・矢印のそばに 軸名 y の文字
・縦軸上に、目盛3つ以上と数値（と単位）
・原点Originに O（オー）



時間 0 分に 0 [km]
時間 10 分に 5 [km]

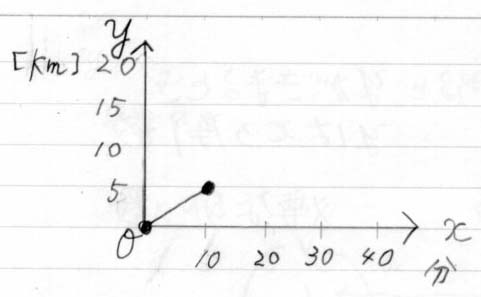
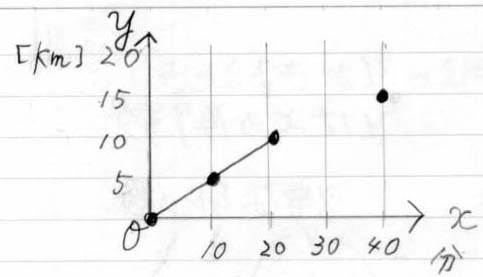
2点打ったら線でつないでください
時間 20 分に 10 [km]
時間 40 分でやっと 15 [km]

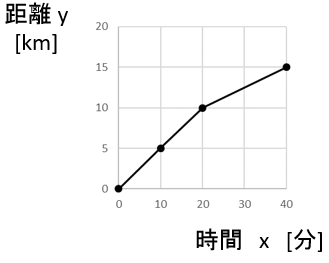
増加率のグラフを書く

今のグラフの真下に、ｘ軸をそろえて、増加率のグラフを書きます。
横軸はさっきと同じですが、縦軸はｙではなく増加率 \(\frac{\Delta y}{\Delta x}　\)にします

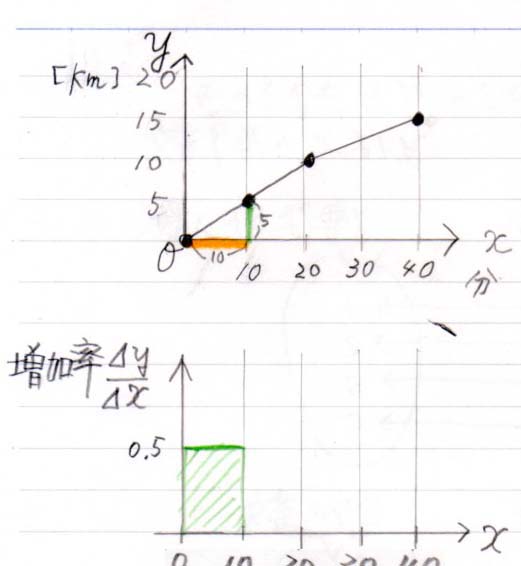
出だしは \( \frac{\Delta y}{\Delta x}　 = \frac{5 [km]}{10 [分]}　=\) 0.5 [km/分]
0分から10分までの「10分間」に、速度 0.5 [km/分] の棒グラフを書いてください。

10分から20分のところも \( \frac{\Delta y}{\Delta x}　 = \frac{5 [km]}{10 [分]}　=\) 0.5 [km/分]

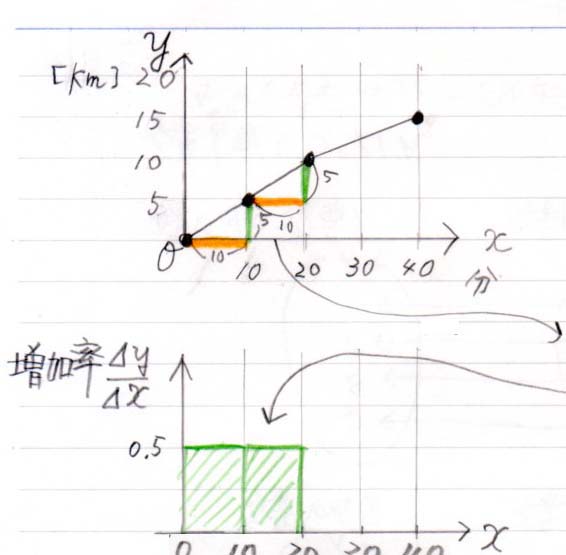
10分から20分までの「10分間」に、速度 0.5 [km/分] の棒グラフを書いてください。

20分から40分は \( \frac{\Delta y}{\Delta x}　 = \frac{5 [km]}{20 [分]}　=\) 0.25 [km/分]

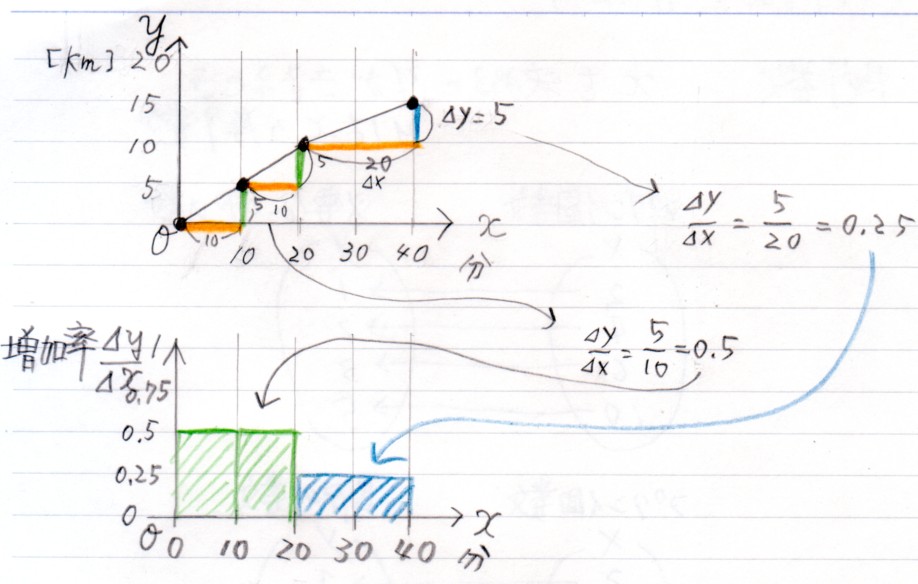
20分から40分までの「20分間」に、速度 0.25 [km/分] の棒グラフを書いてください。

これで、$y$ のグラフ（上）と 増加率\( \frac{\Delta y}{\Delta x}\)のグラフのセットが完成です。

次のページ