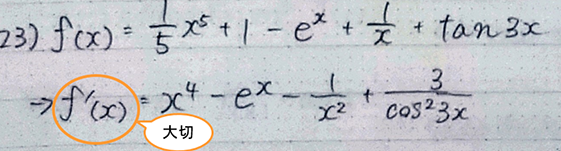-
次の関数を微分しなさい。ただし $a, b$ は定数
-
13) $\displaystyle f(x) = a + \tan( bx ) $
$\qquad \displaystyle f'(x) = 0+ {b\over \cos^2(bx)}$
0+ はかかなくていいです。定数$a$を微分したら0
14) $\displaystyle f(x) = \cos({\pi \over 4}) $
$\qquad \displaystyle f'(x) = 0 $
$x$が出てこない、 $\cos({\pi \over 4}) $は定数です。定数を微分したら0です
15) $\displaystyle f(x) = 4 \sin( 5x ) $
$\qquad \displaystyle f'(x) = 20\cos(5x)$
16) $\displaystyle f(x) = b \cos( ax ) $
$\qquad \displaystyle f'(x) = -ab\sin(ax) $
$\qquad -ba\sin(ax) $ でもべつにかまいません
17) $\displaystyle f(x) = e^{ax} + \tan( bx ) $
$\qquad \displaystyle f'(x) = ae^{ax} + {b\over \cos^2(bx)}$
18) $\displaystyle f(x) = a x^2 + b \sin( 5x ) $
$\qquad \displaystyle f'(x) = 2ax + 5b \cos(5x)$
$\qquad b5 \cos(5x)$ とは書きません。$b$ より数字$5$ が先で$5b$とかきます。
19) $\displaystyle f(x) = 5 + b \cos( ax ) $
$\qquad \displaystyle f'(x) = 0-ab\sin(ax) $
20) $\displaystyle f(x) = a\sin(3x) + \tan( bx ) $
$\qquad \displaystyle f'(x) = 3a\cos{(3x)} + {b\over \cos^2(bx)}$
21) $\displaystyle f(x) = e^{-3x} + a x^3 + \cos( 3ax ) $
$\qquad \displaystyle f'(x) = -3 e^{-3x} + 3a x^2 -3a \sin( 3ax ) $
3項めは、$3a$ という定数がかかっているのですね
22) $\displaystyle f(x) = ax + \tan( ax ) + 2 \cos( (3a+b) x )$
$\qquad \displaystyle f'(x) = a + {a\over \cos^2(ax)} -2(3a+b)\sin{( (3a+b)x )} $
3項めは、$(3a+b)$ を一つの文字として扱えばどうってことないです
23)
-
完璧(5点)
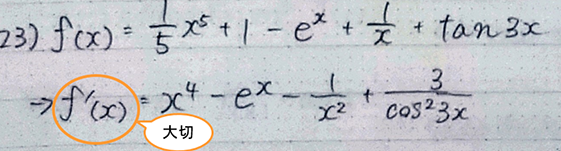
残念 左辺を書き直さないと前の行につながってしまい
誤り

2行目の左辺に f'(x) を書かないと
違う式(微分前の式f(x)と、微分後の式f'(x))を
「等しい」と言っていることになるため、誤りになってしまいます。
15),16), 18)-22)で、定数倍した関数の微分は
単に微分の定数倍になってますが、いいんでしょうか?
定数倍の微分
-
定数$a$として、
\begin{align} \{af(x) \}'
&=& \lim_{h \rightarrow 0} \frac{ \{ a f(x+h) \} - \{ af(x) \} }{h }
\end{align}
共通の定数$a$は外に出せますよね
\begin{align} \{af(x) \}'
&=& \lim_{h \rightarrow 0} \frac{ a \ \{ f(x+h) - f(x) \} }{h }
\end{align}
$a$ は $h$ とも関係ないので、$\lim$ の外に出せて
\begin{align} \{af(x) \}'
&=& a \ \lim_{h \rightarrow 0} \frac{ f(x+h) - f(x) }{h }
\\
\\
&=& a \ f'(x) \qquad \qquad \qquad
\end{align}
定数倍の微分は、微分の定数倍でいいってことですね。なんか当たり前...
つぎのページ
もくじ
|