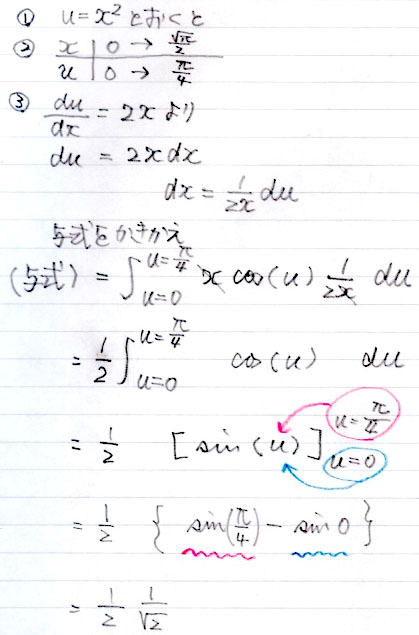-
掛け算の積分は掛け算に微分から行くのでしたね
$ \{ f(x) g(x) \}' = f(x)' g(x) + f(x) g(x) '$
積分して
\begin{align}
\Bigl[ f(x) g(x) \Bigr]_{ x=0から}^{ x={\pi \over 2}まで}
&=
\int_{ x=0から}^{ x={\pi \over 2}まで} f(x)' g(x) \, dx
+
\int_{ x=0から}^{ x={\pi \over 2}まで} f(x) g(x) ' dx
\\
\Bigl[ f(x) g(x) \Bigr]_{ x=0から}^{ x={\pi \over 2}まで}
&-
\int_{ x=0から}^{ x={\pi \over 2}まで} f(x)' g(x) \, dx
=
\int_{ x=0から}^{ x={\pi \over 2}まで} f(x) g(x) ' dx
\\
\end{align}
この式を導出してからやればよいですね
$\displaystyle
\int_{ x=0から}^{ x={\pi \over 2}まで} f(x) g(x) ' dx
=
\Bigl[ f(x) g(x) \Bigr]_{ x=0から}^{ x={\pi \over 2}まで}
-
\int_{ x=0から}^{ x={\pi \over 2}まで} f(x)' g(x) \, dx
$
$f(x)=x, g'(x)= \cos{x}$と考えると $g(x)=\sin{x}$ になるから
\begin{align}
\int_{\Large x=0から}^{\Large x={\pi \over 2}まで} x \cos{(x)} \, dx
&=
\Bigl[ x \sin(x) \Bigr]_{ x=0から}^{ x={\pi \over 2}まで}
-
\int_{ x=0から}^{ x={\pi \over 2}まで} 1 \cdot \sin(x) \, dx
\\
&=
{\pi \over 2}\sin{\pi \over 2} -0\sin{0} - \Bigl[ -\cos{x} \Bigr]_{ x=0から}^{ x={\pi \over 2}まで} \\
& マイナスかけるマイナスのところは見つけ次第プラスに直す \\
&=
{\pi \over 2}\sin{\pi \over 2} -0\sin{0} + \Bigl[ +\cos{x} \Bigr]_{ x=0から}^{ x={\pi \over 2}まで} \\
&=
{\pi \over 2} -0 + \cos{\pi \over 2} -\cos{0} \\
&=
{\pi \over 2} \qquad +\quad 0 \quad -1
\end{align}
$\displaystyle
\int_{\Large x=0から}^{\Large x={\sqrt{\pi} \over 2}まで} x \cos{(x^2)} \, \ dx$
掛け算の積分だし、上の問題と似ているからと思って
$f(x)=x, g'(x)= \cos{(x^2)}$と考えると、
$g(x)$ が分からない!
だいたい、$\cos{(\quad)}$ の( ) の中が $x^2$ なんてやったことない。
ここが1文字だったらできるのに...
...今 大事なこと言いましたよ。「ここが1文字だったら」
こんなときは、
「ここが1文字だったら」の所(今の問題なら$ u = x^2 $)を
$u$ と置いて1文字にすると
うまくいくことがあります。
この方法を置換積分といいます。
置換積分
-
$ u $ と置くと決めたからには、元の式に出てくる$x$ を全部、
$u$ を使って書き換えていきます。
$x$ の出てくる場所は3つ、
(1) 真ん中の被積分関数
(2) 積分区間 $x=0$から $x={\sqrt{\pi} \over 2}$まで
(3) 最後の $dx$
この3つを書いていきます。最初に書くのはさっきの
「ここが1文字だったら」の置き換え
(1)
$u = x^2 $
(2)次に積分範囲をかきなおしていきます。
さっきおいた
$u = x^2 $に代入すると、
$x =0$ の時は
$u =0$
になりますね。そして
$ x ={\sqrt{\pi} \over 2}$ の時は
$ u ={\pi \over 4}$
になりました。
普通はこれを次のような小さい表の形にかきます
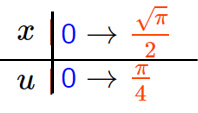
これを使って
$\displaystyle
\int_{\Large x=0から}^{\Large x={\sqrt{\pi} \over 2}まで} $
を
$\displaystyle
\int_{\Large u=0から}^{\Large u={ \pi \over 4}まで} $
に書き換えるのです。
(3) 最後に $dx$ もかきかえます。どうやって?
さっきおいた
$u = x^2 $の両辺を、$x$ で微分します。
そのとき,$ ' $ でなく、
$\displaystyle {d \over dx}$ で書くことがポイントです。
$u = x^2 $ より
$\displaystyle {du \over dx} = 2x $
そしてなんとこれを
$\displaystyle {du } = 2x dx$
$\displaystyle {1\over 2x} du = dx$
と変形するのです。そんなことやっていいの!?
この3つを使って問題の式を書き換えると
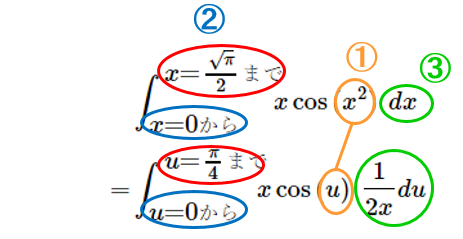
$x$ が約分で消えて

\begin{align}
=&
\int_{\Large u=0から}^{\Large u={ \pi \over 4}まで}
\cos{ (u) } \, \ {1\over 2} du \qquad u だけの式になりました!\\
& 定数の掛け算は外に出してもよいので\\
=& {1\over 2}
\int_{\Large u=0から}^{\Large u={ \pi \over 4}まで}
\cos{ (u) } \, \ du \\
\end{align}
ここまできたらあとは積分できますね。
ノートに書くとこんなかんじ
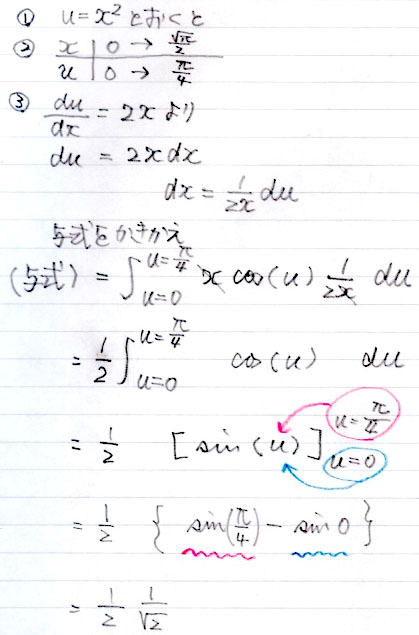
ご注意!この問題は、途中で
$x$ が約分で消えて、$u$ だけの式 にできたので成功しました。
$x$ が消えなくて、
$x$ と $u$ が混ざった式になってしまったときは
この方法は使えません
次のページ
|