-
置換積分ができるのはこんなときです。
-
まえに
$y= f( xの式u )$ の形の微分の時に
\begin{align}
{ df \over dx } = { df\over du} {du \over dx}
\end{align}
と書きましたね。これを積分した形
\begin{align}
\int_{x=aから}^{x=bまで} { df\over du} {du \over dx}
\, dx
\end{align}
になっているときには、$u$ と置き換えるとうまくいきます。
さっきの例も

の形になっていましたね。
- 次の例
-
$\displaystyle
\int_{\Large x=0から}^{\Large x={\pi \over 3}まで} \sin{x}\cos^4{x} \, dx
$
$\cos^4{x} $ とは $(\cos{x})^4$ のことですから、
$u=\cos{x}$ と置いたら $u^4$ とかけますね。
そして嬉しいのは、
$u=\cos{x}$ を微分した $-\sin{x}$ に近い形(符号だけ違う)が
掛け算されてますね!これはうまくいくパターン
やってみて
(1) $u=$
(2) 範囲の書き換え
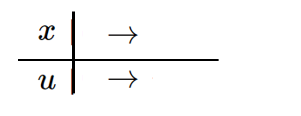
(3) $dx$ の書き換え
$\displaystyle
{du \over dx } = \qquad \qquad $ より
${du } = $
よって
${dx } = $
できたら
めくる
|

