置換積分のよくある間違い
-
$\displaystyle
\int_{\Large x=0から}^{\Large x={\pi \over 3}まで} \cos^3{x} \, dx
$
- 失敗例
-
$u=\cos{x}$ と置きたくなりますが、その微分 $-\sin{x}$がありません。
おかしいなと思いながら強行すると、
(1) $u=\cos{x}$ とおくと
(2) 積分範囲
| $x$ | |
0 $\rightarrow$ ${\sqrt{\pi} \over 3}$ |
| $u$ | |
1 $\rightarrow$ ${ 1 \over 2}$ |
(3) $dx$ の書き換え
$\displaystyle
{du \over dx } = -\sin{x} $ より
${du } = -\sin{x} dx $
${dx } = -{1\over \sin{x}}du $
代入すると
（与式）＝
$\displaystyle
\int_{\Large u=1から}^{\Large u={ 1 \over 2}まで} u^3 (- {1\over \sin{x}}) \, du
$
$\sin{x}$ が消えません！
$u$ と $x$ が混ざった式になって、$u$ だけになりません！
$u$ と $x$ が混ざったら失敗です！ $u$ とおいたら、$u$ の微分がついてないと。
- 成功例
-
ではどうするかというと、３乗を１乗と2乗の掛け算に分け
\begin{align}
\int_{\Large x=0から}^{\Large x={\pi \over 3}まで} \cos^3{x} \, dx
&=
\int_{\Large x=0から}^{\Large x={\pi \over 3}まで} ( \cos{x} )^3 \, dx \\
&=
\int_{\Large x=0から}^{\Large x={\pi \over 3}まで}\cos{x} ( \cos{x} )^2 \, dx \\
\end{align}
$ \cos{x}$ のほうが $u$ の微分になるように変形します。
ここで役立つのが
$
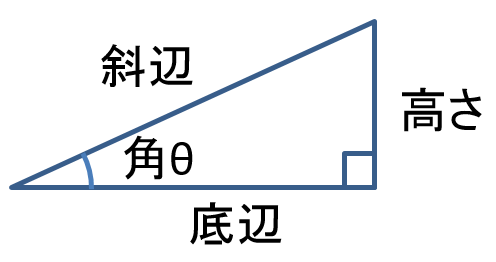\sin ^2{\theta } +
\cos ^2{\theta } = 1
$
$x$でも成り立つので
$
\sin ^2{x } +
\cos ^2{x } = 1
$
よって
$
\cos ^2{x } = 1 -
\sin ^2{x }
$
これより、
\begin{align}
与式
&=
\int_{\Large x=0から}^{\Large x={\pi \over 3}まで}\cos{x} ( 1- \sin^2{x} ) \, dx \\
\end{align}
$\sin{x}$ を $u$ と考えたらできますね。
やってみて
(1) $u=$
(2) 範囲の書き換え
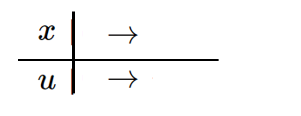
(3) $dx$ の書き換え
$\displaystyle
{du \over dx } = \qquad \qquad $ より
${du } = $
よって
${dx } = $
できたら
めくる
|