- 積分範囲のない「不定積分」の時はどうしたらいいでしょうか。
$\displaystyle
\int x \sqrt{ x^2+1 } \, dx
$
-
ルートの中身を $u$ と置き換えるとうまくいきそうですね
(1) $u= x^2+1$
(2) 範囲の書き換えは、もともと範囲がないので、やらない。
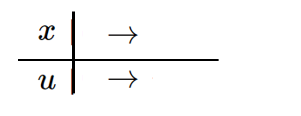
(3) $dx$ の書き換え
$\displaystyle
{du \over dx } = {d \over dx }( x^2+1 ) = 2x+0 $ より
${du } = 2xdx$
よって
${dx } = {1\over 2x} du$
\begin{align}
(与式)
&=
\int x \sqrt{ u } {1\over 2x} \, du \\
&=
\int \sqrt{ u } {1\over 2} \, du \\
&=
{1\over 2} \int \sqrt{ u } \, du \\
&=
{1\over 2} ( {2 \over 3} u\sqrt{ u } +C ) \qquad (Cは任意定数)\\
&=
{1 \over 3} u\sqrt{ u } +{C \over 2} \\
& C は任意なので、{C \over 2}も任意だから C と置きなおすと\\
&=
{1 \over 3} u\sqrt{ u } + C \\
& uを戻して\\
&=
{1\over 3} (x^2+1)\sqrt{ x^2+1 } +C \qquad(完成)\\
& ルートの前の( )がないと誤りです\\
& 次のように書いてもいいです。どっちでもよい\\
&=
{1\over 3} (x^2+1)^{3\over 2} +C \qquad(完成)\\
\end{align}
不定積分の場合は、積分範囲の書き換え場ない代わりに
最後に $u$ を戻す、という操作が入ります。
- 検算
- 得られた式を微分して、与式の中身になればOKです。
$y = {1\over 3} (x^2+1)^{3\over 2} +C $
$u = (x^2+1)$ とおくと
$ y = {1\over 3} u^{3\over 2} +C $
\begin{align}
{ dy \over dx } &= { dy\over du} {du \over dx} \\
&= {1\over 3} ( {3\over 2} u^{1 \over 2}+0) (2x+0)\\
&= u^{1 \over 2} x \\
&= x u^{1 \over 2} \\
&= x \sqrt{u} \\
&= x \sqrt{ x^2+1} \\
\end{align}
与式の中身と同じになったので、OK
- 練習
-
$\displaystyle
\int {2 x + 1 \over \sqrt{ x^2+x+1 } }\, dx
$
-
かいたら
次のページ
|
