- 次のグラフの増加率のグラフを、横軸を揃えてかきなさい
-
出だしはOK、でもよくある間違い
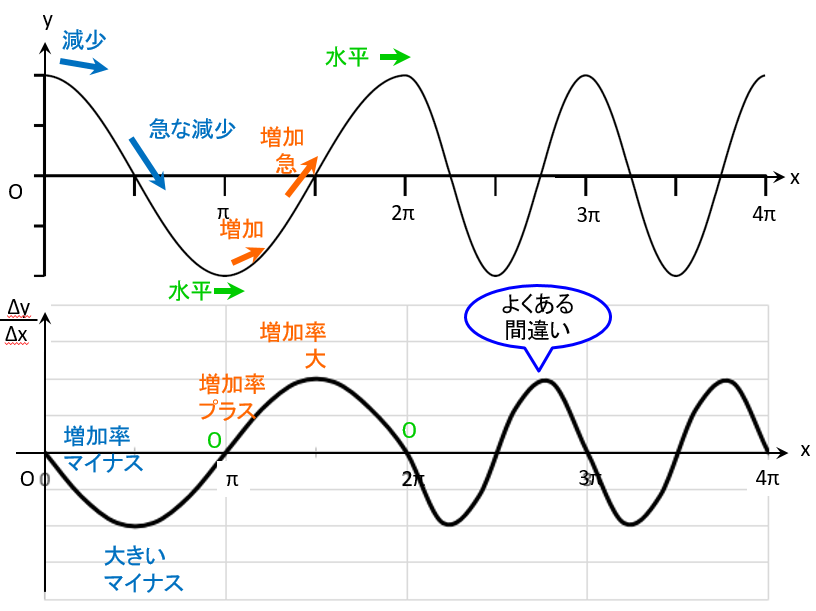
最初は減少なので増加率はマイナス、
だんだん急な減少になるので大きなマイナスになり、
その後、減り方が緩やかになって $x = {\pi}$でどん底、
一瞬水平になるのでここでは増加率は0、
どん底から増加に転じ増加率はプラス、
増加が急になると増加率も大、
だんだん緩やかになって
頂上でまた一瞬傾きがなくなり増加率は0(ここまでOK)、
あと繰り返す、、、、
と、考えがちですが、
- 正しいのはこっち
-
よく見ると、前半に対して後半は同じ長さに波が2つ入っています。
角度が2倍速で進んでいます。
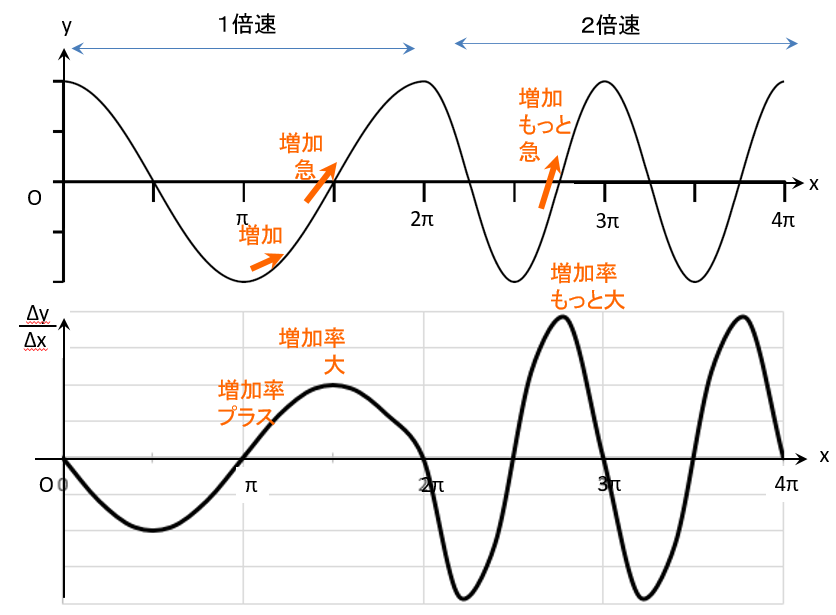
$x= 2 \pi$から3$\pi$にかけて、
普通だったら半周しかしない距離で、すでに1周しちゃってます。
ということは、坂を駆け上がるときも、
半分の距離で同じ高さ上がっているので、
2倍、急な坂ってことです。
ということは、増加率も、2倍なわけですね。
- 式でかくと
-
前半を
$ y = \cos{(x)}$とすると、
後半は
$ y = \cos{(2x)}$ です。角度のところが2倍されているので、2倍速になります。
まだ180°の時に、360°回ったことになっています。
$ y = \cos{(3x)}$ なら3倍速、
$ y = \cos{(4x)}$ なら4倍速、
数字のところが増えれば増えるほど、せわしなく変化する波になっていきます。(高周波といいます)。
ゆったりした変化の波は、低周波です。
では、$ f(x) = \cos{(3x)}$ の導関数を求めてみましょう。
もうひとりでできるんじゃないかな。
かけたらめくる
|

