東北工業大学 工学部情報通信工学科 中川研究室


ラプラス変換

問題例に戻る

例題
インパルス応答		 インダクタンスL=0.5, 抵抗R=20,容量C=0.001のLCR回路に 起電力E=5Vの直流電源がつながっていた。 時刻t=0にこのスイッチを切り換えて、 電源なしの回路にした。 以後の電流と電荷の時間変化を求めよ。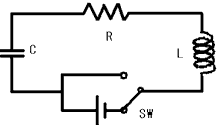
LCR直列、電源あり・なし切り替えただしi(0)=0

回路の問題一覧 　

１．方程式をたてる
抵抗の両端の電圧 R i(t), コイルの両端の電圧 L di(t)/dt, コンデンサ の両端の電圧 q(t)/C, 合計が 電源の起電力E(t)と等しくなるので､

L di(t)/dt + R i(t) + q(t)/C = E(t)


２．両辺をラプラス変換する
L( i ' ) + R( i ) + (1/C)( q ) = ( E )


３．ラプラス変換の微分法則 を使う
Ls( i ) + R( i ) + (1/C)( q ) = ( E ) + Li(0)
 微分法則
( y’ ) =
- y(0) + s ( y )

４．電荷q(t)と電流i(t)の関係を考える
dq(t)/dt = i(t) 　
両辺をラプラス変換
( q ') = ( i ) 　
微分法則を使い
-q(0) + s( q ) = ( i ) 　
　　　　　( q ) ={ ( i ) + q(0) }/s
微分法則
( y’ ) =
- y(0) + s ( y )

５．( i )だけの式にする
( q ) の式を元の方程式に代入して
Ls( i ) + R( i ) + (1/Cs)( i ) + q(0)/Cs
　　　　　　　　　= ( E ) + Li(0)
( i )の出てくる項を左辺にまとめて
( Ls + R + 1/Cs ) ( i )
　　　　　　　　　= ( E ) + Li(0) - q(0)/Cs
( Ls + R + 1/Cs )は
「特性関数」
または
「インピーダンス」

６．右辺を計算する
問題文より i(0) = 0, また、時刻t=0までは電流が無くLとRでの電圧降下が無いので、 電源電圧Eがそのままコンデンサに掛かっていたはずなので､ コンデンサにたまっていた電荷は
q(0)= CE
時刻t=0のスイッチ切り換え以降は電源の無い回路になるので E(t)= 0
( 0 )= 0　なので
( Ls + R + 1/Cs ) ( i ) = 0 + 0 - CE/Cs


７．左辺を( y ) = の形にして整理
( Ls + R + 1/Cs ) ( i ) = -E/s

変形して
( Ls2 + Rs + 1/C )/s ( i ) = -E/s

両辺にs/( Ls2 + Rs + 1/C )をかけ
( i ) = -E/( Ls2 + Rs + 1/C )

変形して
( i ) = -E/L{ s2 + (R/L)s + (1/LC) }

　　ここで初めて数値を代入
E = 5, L = 0.5, R = 20, C =0.001 = 10-3 なので
E/L = 10, R/L = 40、 1/LC = 2×103 です。
よって
( i ) = -10/{ s2 + 40 s + 2000 }
これは
( i ) = -10/{ (s+20)2 -400 +2000 }
ですから
( i ) = -10/{ (s+20)2 +1600 }
つまり
( i ) = -10/{ (s+20)2 + 402 }
の形になるので
( e-あれｔ sin(これｔ) ) = これ/{ (s+あれ)2 + これ2 }
のパターンにもちこめます。
分子に「これ」=40が来て欲しいので､変形して
( i ) = (-1/4)・ 40/{ (s+20)2 + 402 }
８．右辺が何のラプラス変換か考える
( i ) = ( (-1/4)・ e-20ｔ sin(40t) )

９．両辺の(　）を同時にはずす
i = (-1/4)・ e-20ｔ sin(40t)

左の式は
( i ) = ( Ls + R + 1/Cs )-1
ともかけるね。
この( Ls + R + 1/Cs )-1を
「伝達関数」と
いいます

今､ i は
インパルス応答だから
( インパルス応答 )=
　　　　　　( 伝達関数 )
検算しましょう
 出来た答えを微分して元の方程式に代入し、成り立つかどうか確かめよう。
初期条件も代入して確かめよう。ただし、 インパルス応答のときは t=0 を代入して成り立たないこともあります。

解を吟味
 出来た答え
i = (-1/4)・ e-20ｔ sin(40t) )
は、角周波数40のサイン波です。2π/T=40より、周期T=π/20 となります。
しかもこれは e-20ｔ がついてますから時間とともに振幅が減っていく 減衰振動ですね。 減衰のタイムスケールは､20ｔ=1となったときに元の振幅の1/eになるので、 t =1/20 です。
だから、この波形を詳しく観察したいなら､周期π/20 や減衰のタイムスケール1/20より はるかに細かい時間スケールで観察しないといけませんよね。

回路の問題例 　 合成法則 (f)(g) へ進む

「初心者用ラプラス変換解説」最初のページへ戻る

◆中川研HOME