-
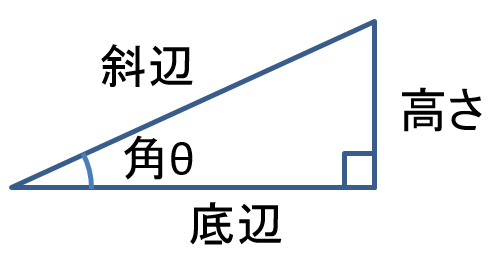
\begin{align} \sin{\theta }= \frac{高さ}{斜辺} , \quad \cos{\theta }= \frac{底辺}{斜辺} \quad \end{align} より \begin{align} {高さ}={斜辺}\sin{\theta }, \quad {底辺}={斜辺} \cos{\theta } \end{align} これをピタゴラスの定理 底辺2+高さ2=斜辺2 に代入すると
\begin{align} ({斜辺} \sin{\theta })^2 + ({斜辺} \cos{\theta })^2 = {斜辺}^2 \end{align} \begin{align} {斜辺}^2 (\sin{\theta })^2 + {斜辺}^2 (\cos{\theta })^2 = {斜辺}^2 \end{align} 両辺を斜辺2で割ると
\begin{align} (\sin{\theta })^2 + (\cos{\theta })^2 = 1 \end{align}
これがとてもとても便利なのでいろいろなところで使います。
複雑な式が、これを使うと超簡単になったりします。
ぜひ使ってください。(教科書p16定理1.1)
ちなみに、
$(\sin{\theta })^2$ のことを $\sin ^2{\theta }$ 、 $(\cos{\theta })^2$ のことを $\cos ^2{\theta }$ と
書いていいことになっているので \begin{align} \sin ^2{\theta } + \cos ^2{\theta } = 1 \end{align}
と書くことが多いです。
次のページ