-
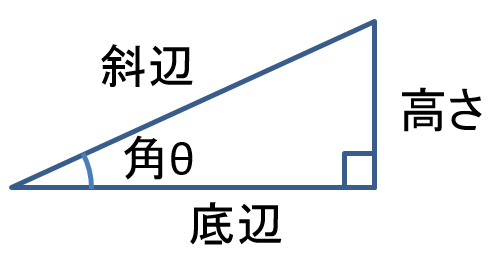
\begin{align} \sin{\theta }= \frac{高さ}{斜辺} , \quad \cos{\theta }= \frac{底辺}{斜辺} \quad \end{align} より \begin{align} {高さ}={斜辺}\sin{\theta }, \quad {底辺}={斜辺} \cos{\theta } \end{align} これを \begin{align} \tan{\theta }= \frac{高さ}{底辺} \quad \end{align} に代入すると
\begin{align} \tan{\theta }= \frac{斜辺 \sin{\theta }}{斜辺 \cos{\theta }}\quad \end{align} 約分すると
\begin{align} \tan{\theta }= \frac{ \sin{\theta }}{ \cos{\theta }}\quad \end{align} これもとても便利です。(教科書p16)
これがあれば、タンジェントがでてきたらコサインとサインの比に直せばいいので
$\tan$の出てくる公式は覚える必要がないです。
たとえば \begin{align} 1+ \tan ^2{\theta } &= 1 + ( \tan{\theta})^2 \\ &= 1 + ( \frac{ \sin{\theta }}{ \cos{\theta }})^2 \\ &= 1 + \frac{ (\sin{\theta)^2 }}{ (\cos{\theta })^2}\\ 通分\\ &= \frac{(\cos{\theta })^2+ (\sin{\theta)^2 }}{ (\cos{\theta })^2} \end{align} ここで分子は $ (\sin{\theta })^2 +(\cos{\theta })^2 = 1$ なので \begin{align} 1+ \tan ^2{\theta } &= \frac{1}{ (\cos{\theta })^2} \quad \end{align} $(\cos{\theta })^2$ のことを $\cos ^2{\theta }$ と書いてもいいので \begin{align} 1+ \tan ^2{\theta } &= \frac{1}{ \cos ^2{\theta }} \quad \end{align} 暗記する必要ないです。計算すれば出ます。(教科書p16定理1.1)
次のページ