-
- 三角比から
三角関数へ
-
いろいろな角度のサインを求めてみると、角度によって値が変わるので
$\sin{\theta}$ は角度 $\theta$ の関数です。
角度を $x$ とするなら、$\sin{(x)}$ は角度 $x$ の関数です。
$\cos{(x)}$ や $\tan{(x)}$ も同じですね。
これらを三角関数といいます。
実習の結果をみると、最初は
角度が大きくなるにつれて$\sin{(x)}$も大きくなっていきましたが
90°を過ぎると今度は減っていきますよね。
このようすをグラフに書いてみたいと思います。
-
$y=\sin(x)$のグラフ
-
ノートまたはグラフ用紙にy=sin(x) のグラフを描いてください。
ノートに書く方は、目盛り 1 つ当たり30°ずつ増えるように
縦軸 y は 0.5 当たり 1行になるよう、上下2行ずつとって軸を書いてください。

方眼紙(グラフ用紙)を持っている方は
B5 版なら横置き、A4 版なら縦置きで
横軸$x$は 1.5cm が30°になるよう
縦軸$y$は 1cm が $y$=1 になるよう、上1 cm 下1 cm の軸を書いてください。

横軸は角度 $x=$ 0°から360°まで、30°間隔に目盛を入れて
そばにその角度のミニチュア三角形を図示してください。
ミニチュア三角形を見ながら、$y=\sin{(x)}$ の値を求めて
点を打ってつないでください。
例:
$x=30$° のとき
$y=\sin{30^\circ} = \frac{1}{2}=0.5$ なので
$x=30$°、$y=0.5$ のところに点を打つ
$x=60$° のとき
$y=\sin{60^\circ} = \frac{\sqrt{3}}{2}= \frac{1.732}{2}=0.866..$ なので
$x=60$°、$y=0.866..$ のところに点を打つ
$\sqrt{3}$の値は、日本人なら
1・7320508
ひとなみにおごれや とおぼえます。(ふつう1.732まであれば十分)
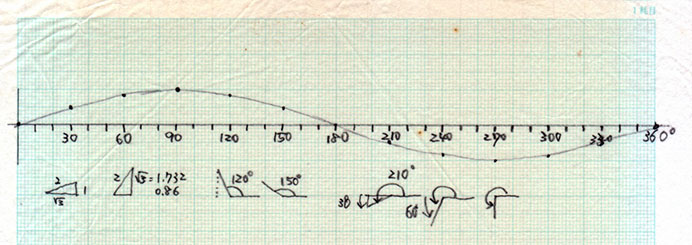
30°60°とか書きやすいところからかいて、
書きづらい0°などはあとから書くと分かりやすいです。
軸名や原点を書いて完成させてください。
-
$y=\cos(x)$のグラフ
-
ノートなら $x$ 軸の6行下に新しい横軸を書き
方眼紙なら $x$ 軸の4cm 下に新しい横軸を書き
同じようにミニチュア三角形と $y=\cos(x)$ のグラフをかいてください。
-
$y=\tan(x)$のグラフ
-
ノートなら $x$ 軸の10行下に新しい横軸を書き
方眼紙なら $x$ 軸の8cm 下に新しい横軸を書き
縦軸はy=2 以上とって
ミニチュア三角形と $y=\tan(x)$ のグラフをかいてください。
$x=90$° のときや
$x=270$° のときは、底辺の長さが0になってしまい、
0で割り算はできないのでかけません。
そんなときは、
$x=89.9$°とか
$x=90.1$°とかの三角形を書いてみて、
「ほぼ1」の高さを0.0001とかの微小な底辺で割ったらどうなるか
を考えてください。
$x=90$°から$x=270$°の範囲は、底辺がマイナスなことにも気を付けて
$y=\tan(x)$のグラフはところどころ切れているので、無理やりつながないこと。
$\frac{1}{\sqrt{3}}$ を計算するときは、いきなり $\frac{1}{1.732...}$ を計算するよりも、
上下に$\sqrt{3}$ をかけて
$\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} = \frac{1.732...}{3} $ を計算するほうが楽ですよね。
グラフ3枚書いたら
次のページ
|


