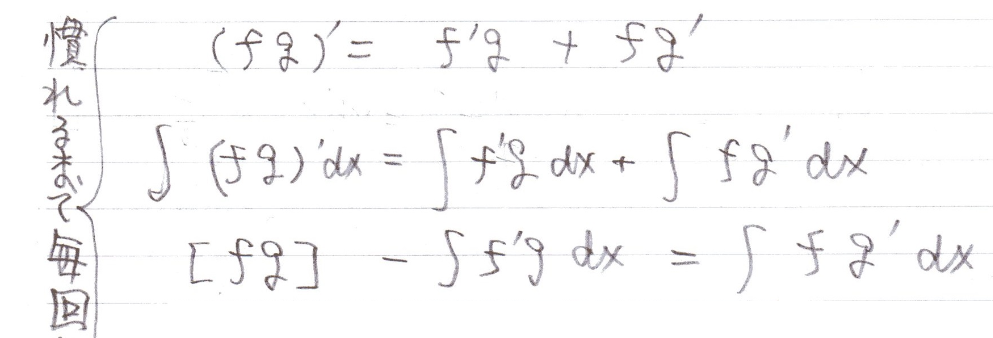- 部分積分
-
$\displaystyle
\int {x \log_e{x} }\ dx \quad
$
掛け算の積分のときは、掛け算の微分の式から
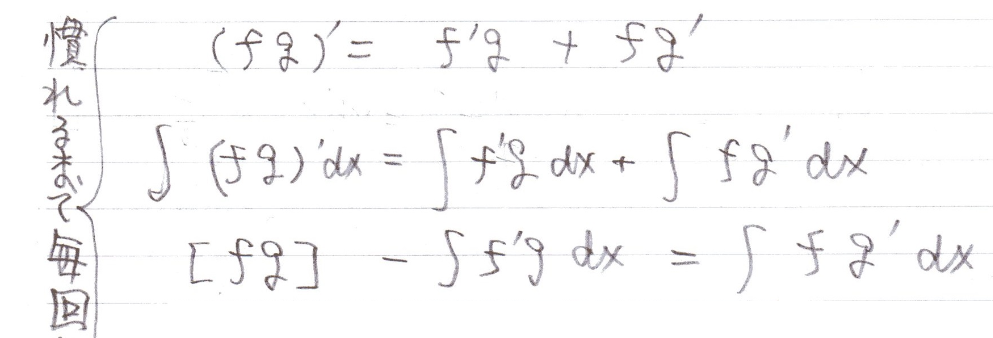
これ毎回書くんでしたね
そして作戦を立てます。どっちを $f$ にしてどっちを $g'$ にするのか。
できない人はここがテキトーなんです。
「たまたま」うまくいく確率は50%しかありません。
そんな不確実なことやってられません。
いつも $x$ のほうを $f$ にすることが多いのは、
微分すると $f'$ が1になって消えてくれるからです。
でも今回、 $x$ のほうを $f$ にすると、
$g'$ が$\log_e{x}$ になってしまい、もとの $g$ がわかりません。
だから
$\log_e{x}$ のほうを、これから微分する $f$ にするのです。
$f(x)=\log_e{x}$
$g'(x) = x $ これならもとの $g$ は簡単、 $g(x) = {x^2\over 2}$
あとは自分の導出した式に入れるだけ
|
\begin{align}
\int f(x) g'(x) dx
=
f(x) g(x)
-
\int f'(x)g(x) dx
\end{align}
|
\begin{align}
\int x \log_e{x} dx
&=
{x^2 \over 2 } \log_e{x}
-
\int ( \log_e{x} )' {x^2 \over 2 } dx \\
\\
&=
{x^2 \over 2 } \log_e{x}
-
\int {1 \over x} {x^2 \over 2 } dx \\
\\
&=
{x^2 \over 2 } \log_e{x}
-
\int {x \over 2 } dx \\
\\
&=
{x^2 \over 2 } \log_e{x}
-
{x^2 \over 4 } +C
\end{align}
積分出来たら検算
\begin{align}
( {x^2 \over 2 } \log_e{x} - {x^2 \over 4 } +C )'
&=
( {x^2 \over 2 })' \log_e{x} +
{x^2 \over 2 } (\log_e{x} )' - ( {x^2 \over 4 } +C )'\\
&=
\end{align}
問題の「被積分関数」$x\log_e{x}$ と同じになったらOK
- 練習
- 教科書p.99 例題41 (1)
- 練習
-
$\displaystyle
\int {1 \over x } \, dx
$
$\displaystyle
\int {1 \over x^2 } \, dx
$
$\displaystyle
\int {1 \over \sqrt{x} } \, dx
$
やってみて
かいたらめくる
|