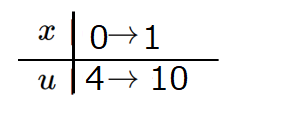- 答え合わせ
-
$\displaystyle
\int_{x=0}^{x=1} {2x+5 \over x^2+5x+4} \, dx
$
分母を $u$ とおいたとき、その微分 $u'$ が掛け算された形
になっているのでうまくいきますね。
(1) $u =x^2+5x+4 $とおくと
(2)
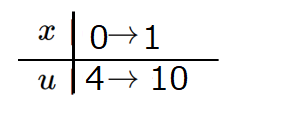
(3)
$\displaystyle {du\over dx } = 2x+5$ より
-
$du = (2x+5) dx$ ここに( )がないと誤り、 2x+5 dx は不可
$dx = {1\over (2x+5)} du$
\begin{align}
\int_{x=0}^{x=1} {2x+5 \over x^2+5x+4} \, dx
&=
\int_{u=4}^{u=10} {2x+5 \over u } {1\over (2x+5)} \, du\\
\\
&=
\int_{u=4}^{u=10} {1 \over u } \, du \quad (uだけになって嬉しい)\\
\\
&=
\Bigl[ \log_e|u| \Bigr]_{u=4}^{u=10} \\
\\
&=
\log_e|10| -\log_e|4|\\
\\
&=
\log_e{10\over 4}\\
\\
&=
\log_e{5\over 2}\\
\end{align}
|