-
\(
f(x) = 3^x\) のグラフと増加率 \( \frac{\Delta y}{\Delta x}\) のグラフ
-
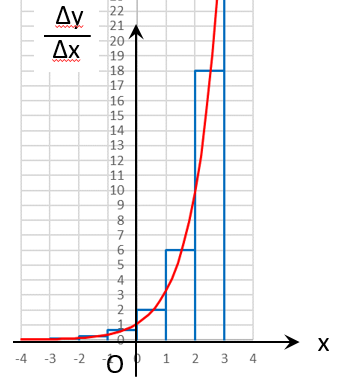
ざっくり \(\Delta x = 1 \) ずつ区切っていくとこんな感じになりますが
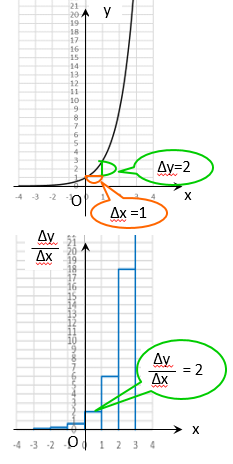
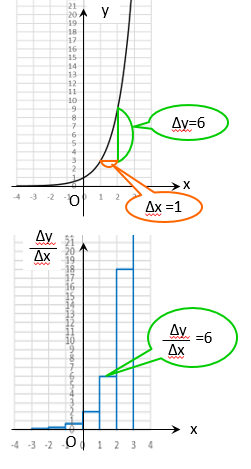
でもこれは\(y= 3^x\) というよりむしろ
「カクカクしたグラフ」の場合であって、なめらかな\(y= 3^x\) のグラフなら
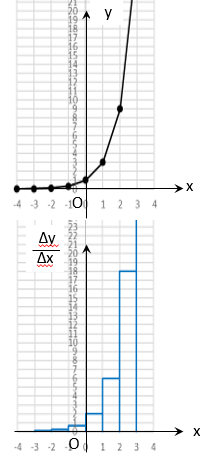
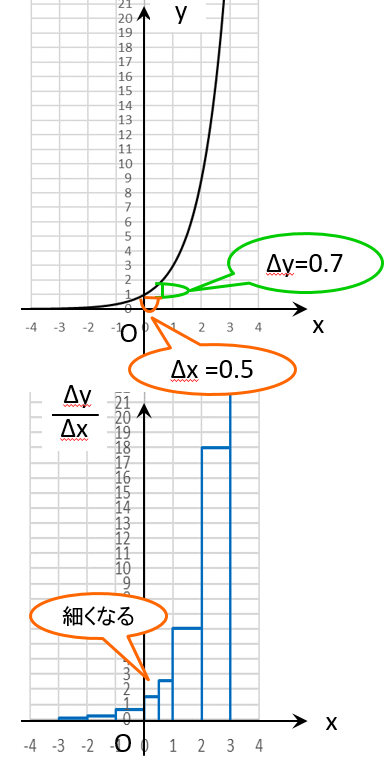
右図のように \(\Delta x \) を細かくすれば、棒グラフは細くなり、
さらに細かくすれば、棒グラフはどんどん細くなり、
増加率のグラフもなめらかになるはずですよね。
例:
$x=0$ から $x = 0.5$ までの区間で
$y=1$ から \(y=3^{1\over 2} = \sqrt{3} \) ( 1.73くらい)まで
\begin{align}
\frac{\Delta y}{\Delta x} = \frac{1.73-1}{0.5-0}= 1.46
\end{align}
例:
$x=0.5$ から $x = 1$までの区間で
\(y= \sqrt{3} \) から$y=3$ まで
\begin{align}
\frac{\Delta y}{\Delta x} = \frac{3-1.73}{1- 0.5}= 2.54
\end{align}
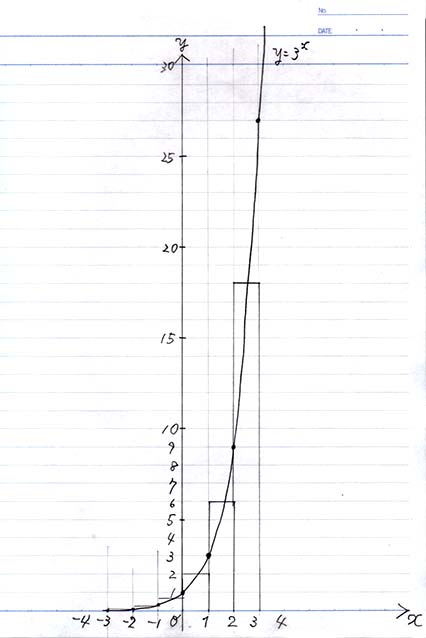
なめらかな増加率のグラフのだいたいの形を書くため、
それぞれの棒グラフの上端の横線の真ん中あたりを
赤い線でなめらかにつないでみてください。
なんかいい感じのグラフになりました。
これ、もともとの\(f(x) = 3^x\) のグラフに似てませんか?
同じかな?
確かめるために、重ねて書きたいと思います。
先に書いた、もともとの\(f(x) = 3^x\) のグラフに重ねて、
増加率の棒グラフを薄く書いて、
例:
$x=-1$ から $x = 0$ までの区間では
$y=3^{-1}$ から $y=1$までなので
\(\Delta y = 1-\frac{1}{3} = \frac{2}{3}\)
$x=-2$ から $x = -1$ までの区間では
$y=3^{-2}$ から $y=3^{-1}$までなので
\(\Delta y = \frac{1}{3}- \frac{2}{9} = \frac{2}{9}\)
:
かいたら
棒グラフの横線の真ん中を赤線で丁寧につないでください。
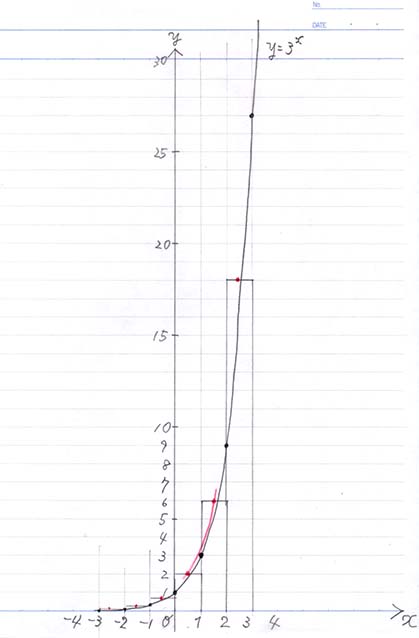
赤線と黒線は重なる?
できたら次のページ
|






